Shallow Neural Networks

Xin chào các bạn, trong bài viết trước chúng ta đã hiểu cơ bản về xây dựng một mạng thần kinh cơ bản với đầu vào và qua 1 lớp activation cho ra kết quả. Trong bài viết này, mình và các bạn sẽ tìm hiểu về mạng lưới thần kinh có 1 lớp ẩn hây được gọi là Shallow Neural Networks.

Mục tiêu của bài viết này:

• Hiểu được hidden units và hidden layers
• Có thể áp dụng một loạt các hàm activation trong một mạng thần kinh
• Xây dựng forward và backward propagation
• Xây dựng và huấn luyện một mạng lưới thần kinh với một lớp ẩn

Neural Networks Overview

Trong hồi quy logistic, mình đã giới thiệu từ bài trước thì mô hình của nó sẽ như sau:

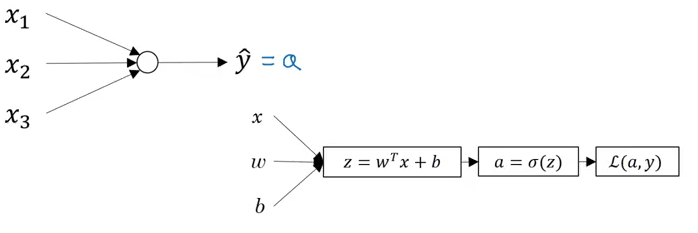
Trong trường hợp mạng thần kinh có một lớp ảnh duy nhất thì cấu trúc của nó sẽ như sau:

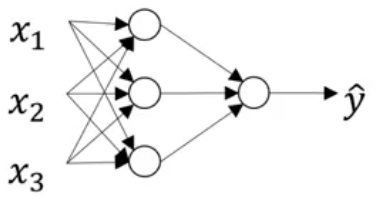
Neural Network Representation

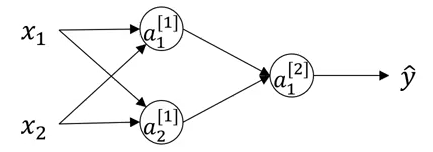
Chúng ta hãy xem xét một đại diện của mạng thần kinh như sau: 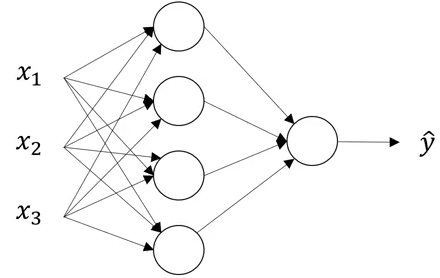Bạn có thể xác định số lượng các lớp ở trên không ? Nhớ rằng trong khi điếm số lượng lớp của NN (Neural Network), chúng ta không đếm lớp đầu vào. Vì vậy trong hình trên có 2 lớp là một lớp ẩn và một lớp đầu ra.

Lớp đầu tiên được gọi là [0] , lớp thứ hai là [1] và lớp cuối cùng là [2] . Ở đây 'a' là viết tắt của kích hoạt (activation), là các giá trị mà các lớp khác nhau của mạng thần kinh truyền sang lớp tiếp theo. Các tham số tương ứng là $W^{[1]},b^{[1]},W^{[2]},b^{[2]}$

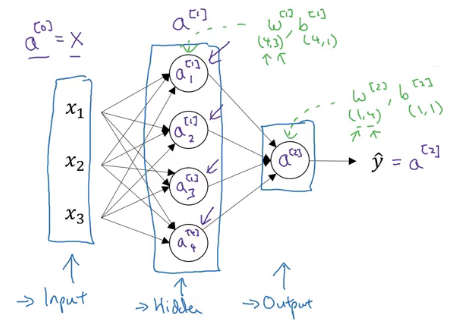
Đây là một mạng thần kinh đại diện. Tiếp theo chúng ta sẽ xem cách tính đầu ra của mạng thần kinh.

Computing a Neural Network’s Output

Chúng ta hãy xem xét chi tiết cách mỗi nơ ron của mạng thần kinh hoạt động. Mỗi nơ ron sẽ nhận một đầu vào, thực hiện 1 số phép biến đổi trên chúng (ở đây là tính $Z=W^{[T]}x+b$) sau đó áp dụng hàm sigmoid:

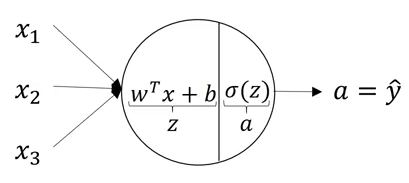
Các bước này sẽ thực hiện trên mỗi tế bào thân kinh. Các phương trình cho lớp ẩn đầu tiên với 4 nơ-ron sẽ là:

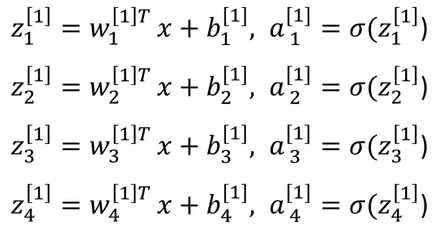
Vì vậy, với đầu vào X đã cho, các đầu ra của lớp 1 và 2 sẽ là:

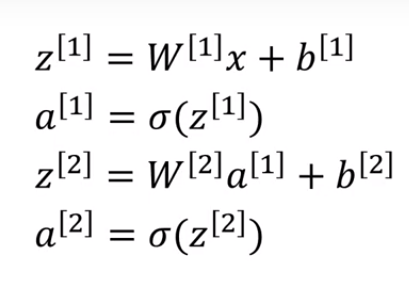
Để tính toán các đầu ra này, chúng ta cần chạy một vòng lặp for sẽ tính toán các giá trị này cho từng nơ ron. Nhưng nhớ lại rằng việc sử dụng vòng lặp for sẽ làm cho việc tính toán rất chậm và do đó chúng ta nên tối ưu hóa mã để loại bỏ vòng lặp này và chương trình chạy nó nhanh hơn.

Vectorizing across multiple examples

Hình thức non-vectorized của đầu ra từ một mạng nơ ron là:

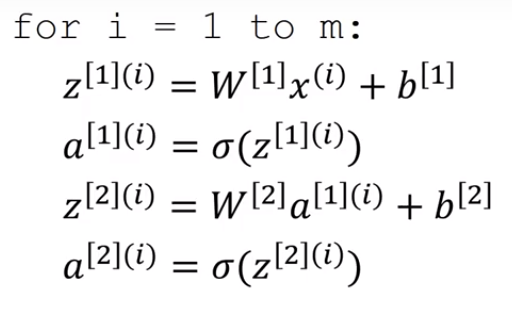
Sử dụng vòng lặp, chúng ta tính Z và giá trị a cho từng ví dụ đào tạo riêng biệt. Bây giờ chúng ta sẽ xem làm thế nào nó có thể được vectorized. Tất cả các ví dụ đào tạo sẽ được hợp nhất trong một ma trận X :

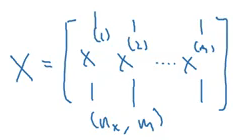
Khi đó đầu ra thheo vectorized sẽ trở thành: 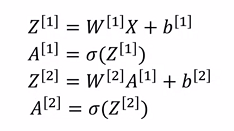Điều này sẽ giảm thời gian tính toán

Activation Function

Trong khi tính toán đầu ra, một hàm kích hoạt được áp dụng. Việc lựa chọn một hàm kích hoạt ảnh hưởng rất lớn đến hiệu suất của mô hình. Cho đến nay, chúng tôi đã sử dụng hàm kích hoạt sigmoid:

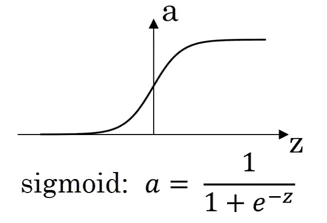
Tuy nhiên, điều này có thể không phải là lựa chọn tốt nhất trong một số trường hợp. Tại sao? Bởi vì ở các cực của đồ thị, đạo hàm sẽ gần bằng 0 và do đó độ dốc giảm dần sẽ cập nhật các tham số rất chậm.

Có các hàm khác có thể thay thế hàm kích hoạt này:

• Tanh

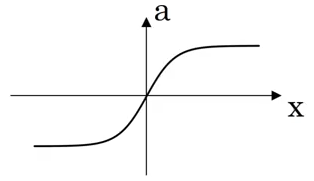
• ReLU

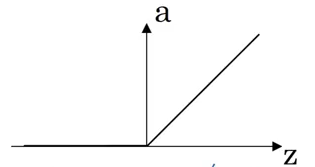
Còn nhiều hàm kích hoạt khác, bạn có thể xem chi tiết công thức tính và đạo hàm của nó trong bảng sau:

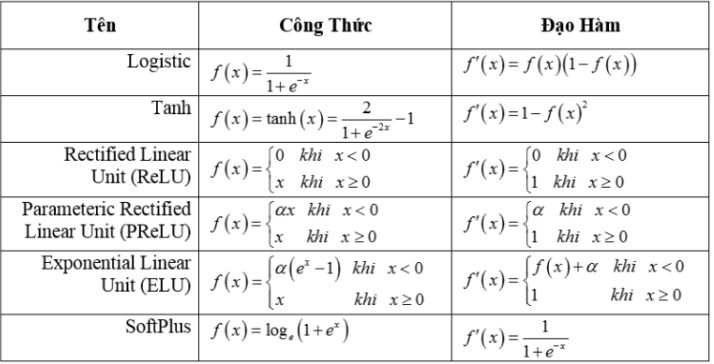
Chúng ta có thể chọn các hàm kích hoạt khác nhau tùy thuộc vào vấn đề chúng ta đang cố gắng giải quyết.

Why do we need non-linear activation functions?

Nếu bạn để ý thì các hàm kích hoạt thường là các hàm phi tuyến tính. Sẽ ra sao nếu chúng ta sử dụng các hàm kích hoạt tuyến tính trên đầu ra của các lớp, nó sẽ tính toán đầu ra dưới dạng một hàm tuyến tính của các tính năng đầu vào. Trước tiên chúng ta tính giá trị Z là: $Z=WX+b$

Trong trường hợp các hàm kích hoạt tuyến tính, đầu ra sẽ bằng Z (thay vì tính toán bất kỳ kích hoạt phi tuyến tính nào): $A=Z$

Sử dụng kích hoạt tuyến tính về cơ bản là vô nghĩa. Thành phần của hai hàm tuyến tính tự nó là một hàm tuyến tính và trừ khi chúng ta sử dụng một số kích hoạt phi tuyến tính, chúng ta không tính toán các giá trị thú vị hơn. Đó là lý do tại sao hầu hết các bài toán sử dụng các chức năng kích hoạt phi tuyến tính.

Một khi chúng ta đã có đầu ra, bước tiếp theo ta sẽ làm gì ? Tất nhiên sẽ là backpropagation để cập nhật lại các trọng số W bằng cách sử dụng gradient descent.

Gradient Descent for Neural Networks

Các tham số mà chúng ta phải cập nhật trong mạng nơ ron hai lớp là: $W^{[1]},b^{[1]},W^{[2]},b^{[2]}$, và hàm chi phí mà chúng ta sẽ giảm thiểu $J$ là:

$$J(W^{[1]},b^{[1]},W^{[2]},b^{[2]})=-\frac{1}{m}\sum _{i=1}^{m}L(\hat{y},y)=-\frac{1}{m}\sum _{i=1}^m\left(y^{(i)}\log \left(a^{[2](i)}\right)+(1-y^{(i)})\log \left(1-a^{[2](i)}\right)\right)$$

Các bước gradient descent có thể được tóm tắt là:

Chúng ta hãy xem forward và backpropagation của một mạng lưới thần kinh 2 lớp sẽ như thế nào. Forward propagation:

$$Z^{[1]}=W^{[1]}\ast X+b^{[1]}$$

$$A^{[1]}=g^{[1]}(Z^{[1]})$$

$$Z^{[2]}=W^{[2]}\ast A^{[1]}+b^{[2]}$$

$$A^{[2]}=g^{[2]}(Z^{[1]})$$

Ở đây các bạn chú ý g(x) chính đại diện cho phép biến đổi dùng hàm kích hoạt, ở đây trong ví dụ này có thể hiểu $g^{[1]}(Z^{[1]})$ chính là $\sigma (z^{[1]})$

Backpropagation:

Đây là các bước hoàn chỉnh mà mạng nơ-ron thực hiện để tạo đầu ra. Lưu ý rằng chúng ta phải khởi tạo các trọng số (W) ở ban đầu. Ta sẽ xem cách khởi tạo các trọng số W như thế nào.

# Random Initialization

Câu hỏi đặt ra khở tạo các trọng số W ban đầu như thế nào? Có thể khởi tạo W là ma trận 0 được không? ó là một câu hỏi thích hợp. Hãy xem xét ví dụ dưới đây:

Nếu các trọng số được khởi tạo thành 0, ma trận W sẽ là:

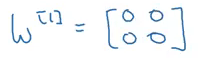
Sử dụng các trọng số này thì : $a_1^{[1]}=a_2^{[1]}$

Và cuối cùng ở bước backpropagation: $d{Z}_1^{[1]}=d{Z}_2^{[1]}$

Cho dù có bao nhiêu đơn vị chúng tôi sử dụng trong một lớp, chúng tôi luôn nhận được cùng một đầu ra tương tự như sử dụng một đơn vị. Vì vậy, thay vì khởi tạo các trọng số về 0, chúng tôi khởi tạo ngẫu nhiên chúng bằng mã sau:

W1 = np.random.randn ((2,2)) * 0,01 
b  = np.zero ((2,1))

Chúng tôi nhân các trọng số với 0,01 để khởi tạo các trọng số nhỏ. Nếu chúng ta khởi tạo trọng lượng lớn, Z sẽ lớn, hàm kích hoạt sẽ ra số lớn ra cực, dẫn đến độ dốc bằng không (trong trường hợp chức năng kích hoạt sigmoid và tanh). Do đó, việc học sẽ chậm. Vì vậy, chúng tôi thường khởi tạo trọng lượng nhỏ một cách ngẫu nhiên.

Reference

Tuần 3 khóa học Nerual Network and Deep Learning

Các slide của tuần 3 khóa học trên tại đây

Conclusion

Vậy là kết thúc bài viết thứ 3, chúng ta đã được giới thiệu về mạng thần kinh có 1 lớp ẩn. Trong bài viết tiếp theo chúng ta sẽ tìm hiểu về Deep Neural Networks cũng tuần cuối của khó học Nerual Network and Deep Learning trên coursera. Cảm ơn bạn đã đọc đến đây, xin chào và hẹn gặp lại trong bài viết sớm nhất