[Thuật toán] Thuật toán minmax (cắt tỉa anpha-beta)

Trong quá trình tìm hiểu thuật toán minmax (cắt tỉa anpha – beta) mình đã tham khảo rất nhiều bài viết và cảm thấy bài viết của QUANG HOANG’S BLOG tương đối dễ hiểu và chi tiết. Rất cảm ơn tác giả về bài viết và xin phép tác giả được trích, tham khảo nội dung về bài viết của mình.

Xét một trò chơi trong đó hai người thay phiên nhau đi nước của mình như cờ vua, cờ tướng, carô,… Trò chơi có một trạng thái bắt đầu và mỗi nước đi sẽ biến đổi trạng thái hiện hành thành một trạng thái mới. Trò chơi sẽ kết thúc theo một quy định nào đó, theo đó thì cuộc chơi sẽ dẫn đến một trạng thái phản ánh có một người thắng cuộc hoặc một trạng thái mà cả hai đấu thủ không thể phát triển được nước đi của mình, ta gọi nó là trạng thái hòa cờ. Ta tìm cách phân tích xem từ một trạng thái nào đó sẽ dẫn đến đấu thủ nào sẽ thắng với điều kiện cả hai đấu thủ đều có trình độ như nhau.

Một trò chơi như vậy có thể được biểu diễn bởi một cây, gọi là cây trò chơi. Mỗi một nút của cây biểu diễn cho một trạng thái. Nút gốc biểu diễn cho trạng thái bắt đầu của cuộc chơi. Mỗi nút lá biểu diễn cho một trạng thái kết thúc của trò chơi (trạng thái thắng thua hoặc hòa). Nếu trạng thái x được biểu diễn bởi nút n thì các con của n biểu diễn cho tất cả các trạng thái kết quả của các nước đi có thể xuất phát từ trạng thái x.

Ví dụ 3-5: Xét trò chơi carô có 9 ô. Hai người thay phiên nhau đi X hoặc O. Người nào đi được 3 ô thẳng hàng (ngang, dọc, xiên) thì thắng cuộc. Nếu đã hết ô đi mà chưa phân thắng bại thì hai đấu thủ hòa nhau. Một phần của trò chơi này được biểu diễn bởi cây sau: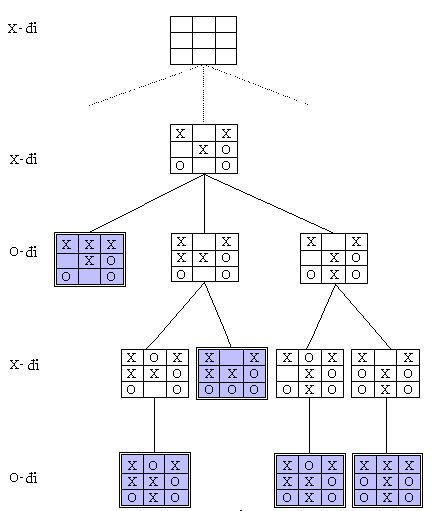

Trong cây trò chơi trên, các nút lá được tô nền và viền khung đôi để dễ phân biệt với các nút khác. Ta có thể gán cho mỗi nút lá một giá trị để phản ánh trạng thái thắng thua hay hòa của các đấu thủ. Chẳng hạn ta gán cho nút lá các giá trị như sau:

· 1 nếu tại đó người đi X đã thắng,

· -1 nếu tại đó người đi X đã thua và

· 0 nếu hai đấu thủ đã hòa nhau.

Như vậy từ một trạng thái bất kỳ, đến lượt mình, người đi X sẽ chọn cho mình một nước đi sao cho dẫn đến trạng thái có giá trị lớn nhất (trong trường hợp này là 1). Ta nói X chọn nước đi MAX, nút mà từ đó X chọn nước đi của mình được gọi là nút MAX. Người đi O đến lượt mình sẽ chọn một nước đi sao cho dẫn đến trạng thái có giá trị nhỏ nhất (trong trường hợp này là -1, khi đó X sẽ thua và do đó O sẽ thắng). Ta nói O chọn nước đi MIN, nút mà từ đó O chọn nước đi của mình được gọi là nút MIN. Do hai đấu thủ luân phiên nhau đi nước của mình nên các mức trên cây trò chơi cũng luânphiên nhau là MAX và MIN. Cây trò chơi vì thế còn có tên là cây MIN-MAX. Ta có thể đưa ra một quy tắc định trị cho các nút trên cây để phản ánh tình trạng thắng thua hay hòa và khả năng thắng cuộc của hai đấu thủ.

Nếu một nút là nút lá thì trị của nó là giá trị đã được gán cho nút đó. Ngược lại, nếu nút là nút MAX thì trị của nó bằng giá trị lớn nhất của tất cả các trị của các con của nó. Nếu nút là nút MIN thì trị của nó là giá trị nhỏ nhất của tất cả các trị của các con của nó.

Quy tắc định trị này cũng gần giống với quy tắc định trị cho cây biểu thức số học, điểm khác biệt ở đây là các toán tử là các hàm lấy max hoặc min và mỗi nút có thể có nhiều con. Do vậy ta có thể dùng kỹ thuật quay lui để định trị cho các nút của cây trò chơi.

Để cài đặt ta có một số giả thiết sau:

· Ta có trường info cho ta giá trị của.
· Các hằng 2 và -2 tương ứng là các trị lớn nhất và nhỏ nhất của từng nút.
· Một biến c kiểu char để xác định định trị cho nút là X hay O đi.
· Một kiểu pointer được khai báo một cách thích hợp để biểu diễn cho một nút trên cây phản ánh một trạng thái của cuộc chơi.
· Ta có một hàm nutLa() để xác định xem một nút có phải là nút lá hay không?
· Hàm max và min tương ứng lấy giá trị lớn nhất và giá trị nhỏ nhất của hai giá trị.

Giải thuật vét cạn định trị cây trò chơi
Hàm val nhận vào một nút q và ký tự c trả về giá trị của nút.

Nếu nút q là nút lá thì trả về giá trị đã được gán cho nút lá. Ngược lại ta cho q một giá trị tạm value là -2 hoặc 2 tùy thuộc q là nút X hay O và xét con của q. Sau khi một con của q có giá trị V thì đặt lại val = max(val,V) nếu q là nút X và value = min(val,V) nếu q là nút O. Khi tất cả các con của q đã được xét thì giá trị tạm val của q trở thành giá trị của nó.

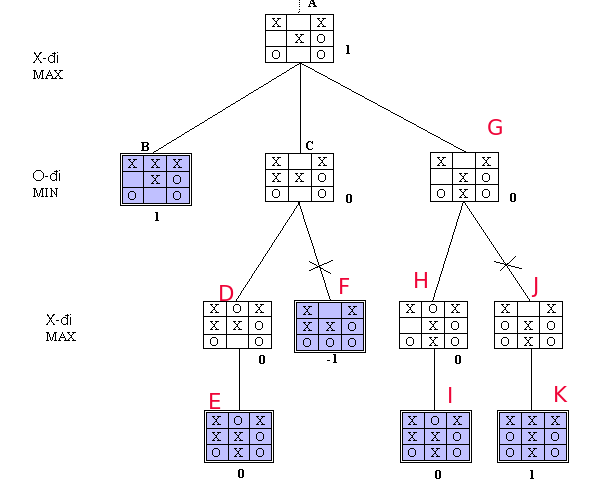
{Ham tra ve gia tri trang thai khi dung minmax - thuat toan minmax}
function val(var q: pointer; c: char; Vp: item): item;
var
	i: integer;
begin
	if (nutLa(q)) then      {Neu la nut la thi lay ngay KQ gia tri cua nut do}
        begin
                {writeln(q^.lab,'->>> ', q^.info);}
                val:= q^.info;
        end
	else
	begin
		for i:= 1 to q^.numChild do   {Duyet cac nut con cua q}
		begin
			if c = 'X' then       {Neu dang la luot X}
			begin
				q^.info:= max(q^.info, val(q^.child[i], 'O', q^.info));
				{writeln(q^.lab,'->>> ', q^.info);}
				val := q^.info;
            end
			else                    {Nguoc lai la luot O}
			begin
				q^.info:= min(q^.info, val(q^.child[i], 'X', q^.info));
				{writeln(q^.lab,'->>> ', q^.info);}
				val := q^.info;
				break;
			end;
		end;
	end;
end;

Áp dụng vào cây tổng quát T ta có cài đặt:

procedure catTia(var T: pointer);  {Dua thuat toan vao cay}
var
	p: pointer;
	i: integer;
begin
	if T <> nil then
	begin
		T^.info := val (T, 'X', T^.info);
	end;
end;

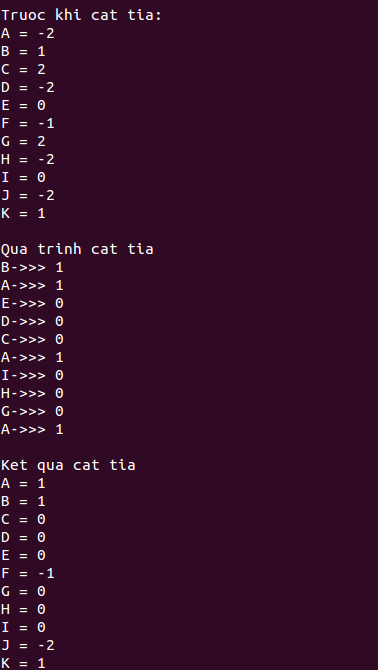
Chuơng trình hoàn chỉnh các bạn có thể xem tại đây

Đọc thêm: Cây tổng quát