UPGRANET spoj – VOI 2011 Nâng cấp mạng
Nguồn đề bài: http://vn.spoj.com/problems/UPGRANET/ 1. Đề bài UPGRANET spoj Một hệ thống gồm n máy tính đánh số từ 1 đến n được kết nối thành một mạng bởi m đoạn cáp mạng đánh số từ 1 đến m. Đoạn cáp mạng thứ i có thông lượng w i kết nối hai máy u i , v i cho phép truyền dữ ...
Nguồn đề bài: http://vn.spoj.com/problems/UPGRANET/
1. Đề bài UPGRANET spoj
Một hệ thống gồm n máy tính đánh số từ 1 đến n được kết nối thành một mạng bởi m đoạn cáp mạng đánh số từ 1 đến m. Đoạn cáp mạng thứ i có thông lượng wi kết nối hai máy ui, vi cho phép truyền dữ liệu theo cả hai chiều giữa hai máy này.
Một dãy các máy x1, x2, …, xp trong đó giữa hai máy xj và xj+1 (j = 1, 2, …, p-1) có đoạn cáp nối được gọi là một đường truyền tin từ máy x1 tới máy xp. Thông lượng của đường truyền tin được xác định như là thông lượng nhỏ nhất trong số các thông lượng của các đoạn cáp mạng trên đường truyền. Giả thiết là mạng được kết nối sao cho có đường truyền tin giữa hai máy bất kì và giữa hai máy có không quá một đoạn cáp mạng nối chúng.
Người ta muốn nâng cấp mạng bằng cách tăng thông lượng của một số đoạn cáp nối trong mạng. Để tăng thông lượng của mỗi đoạn cáp mạng thêm một lượng d (d > 0) ta phải trả một chi phí đúng bằng d. Việc nâng cấp mạng phải đảm bảo là sau khi hoàn tất, thông lượng của mỗi đoạn cáp mạng i đều bằng thông lượng của đường truyền tin có thông lượng lớn nhất từ máy ui tới máy vi.
Yêu cầu
Tìm phương án nâng cấp các đoạn cáp mạng sao cho tổng chi phí nâng cấp là nhỏ nhất.
Dữ liệu
- Dòng thứ nhất: Chứa hai số nguyên dương n, m (n, m <= 10^5).
- Dòng thứ i trong số m dòng tiếp theo chứa ba số nguyên dương ui, vi, wi (wi <= 10^6),
i = 1, 2, …, m.
Các số trên cùng một dòng được ghi cách nhau ít nhất một dấu cách.
Kết quả
ghi ra một số nguyên duy nhất là tổng chi phí nâng cấp theo phương án tìm được.
Ví dụ
| Dữ liệu | Kết quả |
| 6 7 1 2 6 1 3 5 2 4 3 3 4 9 4 5 4 4 6 8 5 6 7 | 5 |
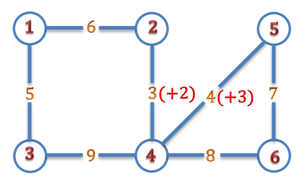
Ràng buộc: 50% số test ứng với 50% số điểm của bài có n <= 100.
2. Thuật toán UPGRANET spoj
Bài này đề hơi khó hiểu một chút. Tức là giữa 2 đỉnh u,v có nhiều đường truyền tin, và có thể có 1 đường nối trực tiếp. Việc ta cần làm là tăng thông lượng của đoạn đường nối trực tiếp đó lên bằng thông lượng of đường truyền tin có thông lượng max từ u đến v.
Có thể sử dụng nhiều thuật toán khác nhau. Ở đây mình sử dụng kruskal để tìm cây khung max. Sau đó, với mỗi cạch không thuộc cây khung có độ dài là c:
Gọi 2 mút của cạnh này là u,v. dùng lca để tìm độ dài đoạn có thông lượng p min trên đường tuyền tin từ u tới v. Khi đó ta phải tăng thông lượng đoạn có độ dài c lên một lượng là p-c.
Ok men!
Không hiểu rõ có thể cmt hỏi nha! <3
3. Code mẫu UPGRANET spoj
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 | #include <bits/stdc++.h> #define oo 1000000000 #define fs first #define sc second using namespace std; typedef pair<int,int> II; typedef pair<int,II> III; III a[100001]; int n,m,deg[100001],lt[100001],sl[100001],d[100001]; vector<II> g[100001]; long long ds=0; int pre[100001],depth[100001],cur[100001],s[100001], valp[100001]; int f[100001][20],vmin[100001][20],retmin; void dfs() { for(int i=1; i<=n; i++) lt[i]=0; int sn=0; s[++sn]=1; lt[1]=1; while(sn) { int u=s[sn]; while(cur[u]<deg[u]&<[g[u][cur[u]].first]) cur[u]++; if(cur[u]==deg[u]) sn--; else{ int v=g[u][cur[u]].first; lt[v]=1; s[++sn]=v; depth[v]=depth[u]+1; pre[v]=u; valp[v]=g[u][cur[u]].second; } } } void init() { for(int i=1; i<=n; i++){ f[i][0]=pre[i]; vmin[i][0]=valp[i]; } int m=int(log2(n))+1; for(int k=1; k<=m; k++) for(int i=1; i<=n; i++) { f[i][k]=f[f[i][k-1]][k-1]; if(f[i][k]==0) vmin[i][k]=oo; else vmin[i][k]=min(vmin[i][k-1],vmin[f[i][k-1]][k-1]); } } void lca(int u, int v) { while(depth[u]>depth[v]) { int k=int(log2(depth[u]-depth[v])); retmin=min(retmin,vmin[u][k]); u=f[u][k]; } while(depth[v]>depth[u]) { int k=int(log2(depth[v]-depth[u])); retmin=min(retmin,vmin[v][k]); v=f[v][k]; } if(u==v) return; int m=int(log2(depth[u]))+1; for(int k=m; k>=0; k--) if(f[u][k]!=f[v][k]) { retmin=min(retmin,vmin[u][k]); retmin=min(retmin,vmin[v][k]); u=f[u][k]; v=f[v][k]; } retmin=min(retmin,vmin[u][0]); retmin=min(retmin,vmin[v][0]); u=f[u][0]; v=f[v][0]; return; } int tim(int u) { if(u==lt[u]) return u; lt[u]=tim(lt[u]); return lt[u]; } int main() { //freopen("upgranet.inp","r",stdin); //freopen("upgranet.out","w",stdout); ios::sync_with_stdio(false); cin>>n>>m; for(int i=1; i<=m; i++) cin>>a[i].sc.fs>>a[i].sc.sc>>a[i].fs; sort(a+1,a+m+1); for(int i=1; i<=n; i++) lt[i]=i,sl[i]=1; for(int i=m; i>=1; i--) { int u1=a[i].sc.fs; int v1=a[i].sc.sc; int u=tim(u1); int v=tim(v1); if(u!=v) { d[i]=1; if(sl[u]<sl[v]){lt[u]=v;sl[v]+=sl[u];} else {lt[v]=u;sl[u]+=sl[v];} deg[u1]++;g[u1].push_back(II(v1,a[i].fs)); deg[v1]++;g[v1].push_back(II(u1,a[i].fs)); } } dfs(); init(); for(int i=1; i<=m; i++) if(d[i]==0) { retmin=oo; int u=a[i].sc.fs; int v=a[i].sc.sc; lca(u,v); int p=retmin-a[i].fs; ds+=(long long)p; } cout<<ds; } |
