Artificial Intelligence - Uninformed search (AI to ML part 3)
Chào mọi người, hôm nay mình sẽ bắt đầu với 1 vài giải thuật tìm kiếm cơ bản nhất trong trí tuệ nhân tạo nhé. Trước tiên, vì sao chúng ta cần biết về các giải thuật tìm kiếm: Ví dụ 1: Tìm tên bài hát (ez => tìm kiếm) Ví dụ 2: Đang ở Bách Khoa muốn tìm đường sang Nông Nghiệp tán gái (tìm kiếm ...
Chào mọi người, hôm nay mình sẽ bắt đầu với 1 vài giải thuật tìm kiếm cơ bản nhất trong trí tuệ nhân tạo nhé. Trước tiên, vì sao chúng ta cần biết về các giải thuật tìm kiếm: Ví dụ 1: Tìm tên bài hát (ez => tìm kiếm) Ví dụ 2: Đang ở Bách Khoa muốn tìm đường sang Nông Nghiệp tán gái (tìm kiếm tiếp) Ví dụ 3: Đang xem bộ phim (JA) này, muốn xem những bộ tương tự quá nhưng éo biết làm thế nào (tìm kiếm tiếp để đưa ra gợi ý) Mọi người thấy đấy, tìm kiếm ở khắp mọi nơi, và tìm kiếm giải quyết hàng tá vấn đề, đến nói mình đi học còn nghĩ, quanh quẩn học máy và trí tuệ nhân tạo chỉ có tìm kiếm, tìm kiếm và tìm kiếm (thật ra không phải vậy =))).
- Xác định mục tiêu cần đạt đến:
- Là một tập hợp các trạng thái đích
- Dựa trên trạng thái hiện tại của môi trường và đánh giá hiệu quả hành động của tác tử
- Phát biểu bài toán Với một mục tiêu cần xác định các hành động và trạng thái cần xem xét
- Quá trình tìm kiếm
- Xem xét các chuỗi hành động có thể
- Chọn các chuỗi hành động tốt nhất
Đây là 1 ví dụ kinh điển mình lấy trong slide của thầy giáo (mà chắc thầy cũng lấy của 1 bài báo nào đó :v) Tình huống:
- Một người đang trong chuyến du lịch ở Rumani
- Ngày mai anh ta có chuyến bay khời hành từ Bucharest
- Bây giờ anh ta cần lái xe để đi từ Arad đến Bucharest
====> Mục tiêu bài toán: Có mặt ở Bucharest, tìm đường đi ngắn nhất (các thành phố cần đi qua)
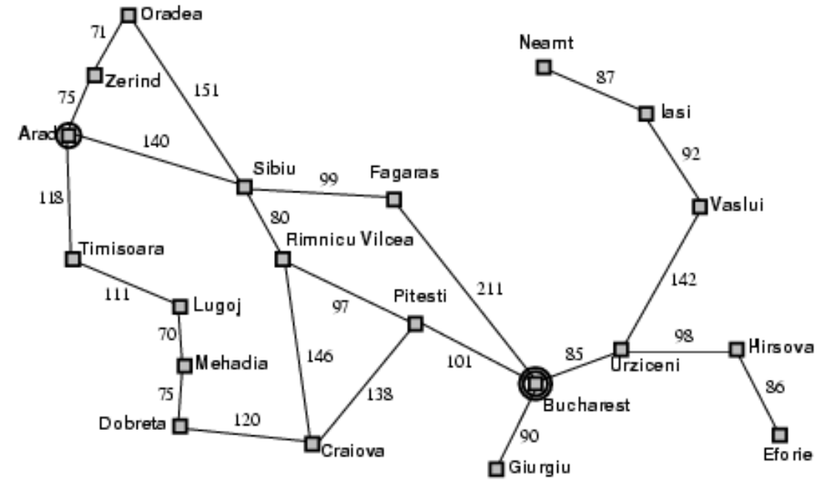 Ví dụ lời giải có thể là: Arad -> Sibiu -> Fagaras -> Bucharest
Được rồi, như hình trên, mỗi thành phố là một điểm trên đồ thị và mỗi thành phố là 1 node, liên kết giữa các thành phố là link, chỉ số trên mỗi link là chi phí để đi từ node này qua node kia. Ta có thể thay đồ thị thành dạng cây như sau:
Ví dụ lời giải có thể là: Arad -> Sibiu -> Fagaras -> Bucharest
Được rồi, như hình trên, mỗi thành phố là một điểm trên đồ thị và mỗi thành phố là 1 node, liên kết giữa các thành phố là link, chỉ số trên mỗi link là chi phí để đi từ node này qua node kia. Ta có thể thay đồ thị thành dạng cây như sau:
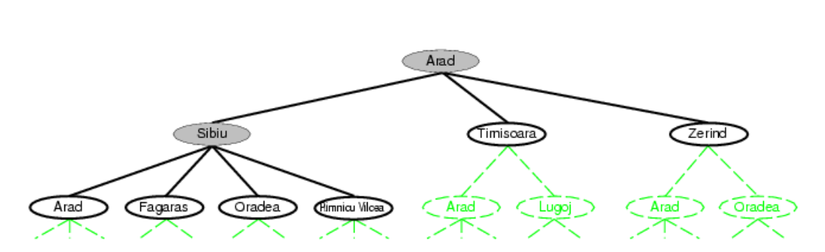 Bài hôm nay mình sẽ không đề cập đến chi phí giữa các node vôi, mình coi như chi phí giữa các node là 1 và chúng ta sẽ tìm hiểu 2 giải thuật tìm kiếm cơ bản nhất, đó là tìm kiếm theo chiều rộng và tìm kiếm theo chiều sâu.
Trước khi đi vào cụ thể, ta sẽ có 1 vài tiêu chí để đánh giá chiến lược tìm kiếm như sau:
Bài hôm nay mình sẽ không đề cập đến chi phí giữa các node vôi, mình coi như chi phí giữa các node là 1 và chúng ta sẽ tìm hiểu 2 giải thuật tìm kiếm cơ bản nhất, đó là tìm kiếm theo chiều rộng và tìm kiếm theo chiều sâu.
Trước khi đi vào cụ thể, ta sẽ có 1 vài tiêu chí để đánh giá chiến lược tìm kiếm như sau:
- Tính hoàn chỉnh
- Độ phức tạp về thời gian (số lượng node được sinh ra)
- Độ phức tạp về bộ nhớ (số lượng node tối đa được lưu trong bộ nhớ)
- TÍnh tối ưu (đảm bảo được chi phí thấp)
Độ phức tạp về thời gian được đánh giá bởi:
- b: hệ số phân nhánh tối đa của cây tìm kiếm
- d: độ sâu của lời giải có chi phí thấp nhất
- m độ sâu tối đa của không gian trạng thái
Ý tưởng: Các node trong cây được xét theo thứ tự độ sâu tăng dần.
Để dễ hiểu, mình có 1 cây đồ thị như sau:
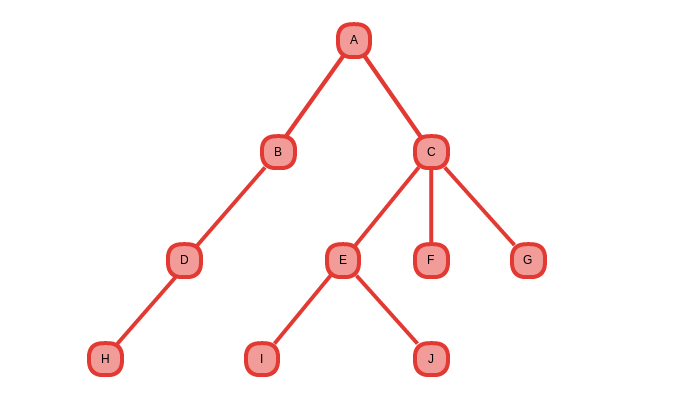 Bài toán đặt ra, tìm đường đi từ A đến F.
Giải thuật:
BFS là giải thuật sử dụng một cấu trúc hàng đời để tìm kiếm node đích. Các thuật ngữ trong giải thuật:
Bài toán đặt ra, tìm đường đi từ A đến F.
Giải thuật:
BFS là giải thuật sử dụng một cấu trúc hàng đời để tìm kiếm node đích. Các thuật ngữ trong giải thuật:
- fringe: cấu trúc hàng đợi lưu trữ các node sẽ đc duyệt
- closed: các node đã đc duyệt
- G=(N, A): cây biểu diễn không gian trạng thái của bài toán
- N0: node gốc của cây
- DICH: tập các trạng thái đích của bài toán
- Γ (n): tập các node con của node đang xét
Giải thuật:
 Ok, để mình giải thích nó hoạt động như thế nào với cái đồ thị đỏ đỏ bên trên nhé.
Đầu tiên, fringe đưa node A vào, sau đó bắt đầu vòng lặp với mục tiêu tìm ra đường đi đến node F
Ok, để mình giải thích nó hoạt động như thế nào với cái đồ thị đỏ đỏ bên trên nhé.
Đầu tiên, fringe đưa node A vào, sau đó bắt đầu vòng lặp với mục tiêu tìm ra đường đi đến node F
| fringe | closed | n |
|---|---|---|
| A | nil | nil |
| B,C | A | A |
| C,D | A,B | B |
| D,E,F,G | A,B,C | C |
| E,F,G,H | A,B,C,D | D |
| F,G,H,I,J | A, B,C,D,E | E |
| G,H,I,J | A,B,C,D,E,F | F |
vậy đường đi là A -> C -> F
Ý tưởng: các node trong cây được xét theo thứ tự độ sâu giảm dần
Quay lại cây đồ thị cũ:
 Bài toán đặt ra, tìm đường đi từ A đến F.
Giải thuật:
DFS là giải thuật sử dụng một cấu trúc ngăn xếp để tìm kiếm node đích. Các thuật ngữ trong giải thuật giống như trong giải thuật BFS
Bài toán đặt ra, tìm đường đi từ A đến F.
Giải thuật:
DFS là giải thuật sử dụng một cấu trúc ngăn xếp để tìm kiếm node đích. Các thuật ngữ trong giải thuật giống như trong giải thuật BFS Sau đây là diễn giải chi tiết cách thức hoạt động
Sau đây là diễn giải chi tiết cách thức hoạt động
| fringe | closed | n |
|---|---|---|
| A | nil | nil |
| B,C | A | A |
| D,C | A,B | B |
| H,C | A,B,D | D |
| C | A,B,D,H | H |
| E,F,G | A, B,D,H,C | C |
| I,J,F,G | A, B,D,H,C,E | E |
| J,F,G | A,B,D,H,C,E,I | I |
| F,G | A,B,C,D,H,C,E,I,J | J |
| G | A,B,C,D,H,C,E,I,J,F | F |
| A,B,C,D,H,C,E,I,J,F,G | G |
Thứ tự duyệt: G -> F -> J -> I ... -> ....B -> A
Ôi viết mấy cái này mệt quá, lần sau mình sẽ đi vào mấy giải thuật siêu hơn chút nhé, sẽ có chi phí đường đi giữa các node, và sẽ duyệt những cây phức tạp hơn
