ìm Node MAX và MIN trong cây nhị phân tìm kiếm - Cấu trúc cây
Trong hướng dẫn này mình sẽ giới thiệu các bạn cách tìm giá trị MAX và MIN trong cây nhị phân tìm kiếm. Đối với cây nhị phân tìm kiếm thì việc tìm ra giá trị lớn nhất và nhỏ nhất trong cây rất đơn giản. Chúng ta sẽ thực hiện một vài cách tìm ra giá trị MAX và MIN để xem cách nào tối ưu nhất. Để ...
Trong hướng dẫn này mình sẽ giới thiệu các bạn cách tìm giá trị MAX và MIN trong cây nhị phân tìm kiếm. Đối với cây nhị phân tìm kiếm thì việc tìm ra giá trị lớn nhất và nhỏ nhất trong cây rất đơn giản.
Chúng ta sẽ thực hiện một vài cách tìm ra giá trị MAX và MIN để xem cách nào tối ưu nhất. Để làm được các bạn cần có kiến thức cơ bản về C++ và các nẵm vững cấu trúc dữ liệu cây.
1. Tìm giá trị MAX trong cây nhị phân tìm kiếm
Trong phần này mình sẽ thực hiện hai cách để tìm ra giá trị MAX trong cây nhị phân tìm kiếm. Các bạn hãy theo dõi và xem thử cách nào tối ưu nhất nhé.
Cách 1:
Trong cách này mình sẽ sử dụng biến toàn cục INT_MIN để giá cho biến MAX, sau đó so sánh với các Node trong cây để tìm ra giá trị lớn nhất, cụ thể như sau:
//------cách 1------------
int MAX = INT_MIN; // gán cho biến MAX là giá trị nhỏ nhất của kiểu integer
//// hàm tìm phần tử lớn nhất trong cây
void TimMax(TREE t)
{
if (t != NULL)
{
// xử lí
if (MAX < t->data)
{
MAX = t->data; // cập nhật lại giá trị cho biến MAX
}
TimMax(t->pLeft);
TimMax(t->pRight);
}
}Ta sẽ sử dụng giá trị nhỏ nhất của kiểu integer và gán cho biến MAX, sau đó ta xét điều kiện nếu cây tồn tại phần tử thì ta thực hiện so sánh MAX với t -> data. Nếu MAX < t -> data thì ta cập nhật lại biến MAX, ngược lại ta sẽ đệ quy để duyệt sang trái và sang phải.
Tuy nhiên đây là một cách không tối ưu, vì chúng ta cần phải duyệt từ đầu đến cuối cây. Vì vậy các bạn hãy xem cách hai mình thực hiện, sẽ nhanh hơn rất nhiều nhé.
Cách 2
Như các bạn đã học thì cây nhị phân tìm kiếm có một cấu trúc lưu trữ dữ liệu rất đặc biệt, vì vậy ta sẽ dựa vào đó để thực hiện tìm ra giá trị MAX một cách nhanh nhất có thể.
Cây nhị phân tìm kiếm luôn luôn lưu giá trị nhỏ hơn ở cây con trái và giá trị lớn hơn ở cây con phải, vì vậy thay vì ta duyệt hết cả cây, ta chỉ cần duyệt sang cây con phải là có thể tìm ra giá trị MAX được rồi.
Các bạn hãy chú ý rằng giá trị ngoài cùng của cây con trái luôn luôn là giá trị nhỏ nhất và giá trị ngoài cùng của cây con phải luôn luôn là giá trị lớn nhất. Dựa vào điều này ta cho hàm duyệt sang bên cây con phải đến giá trị ngoài cùng nhất, khi đó giá trị MAX chính là t -> data của Node ngoài cùng.
int TimMax(TREE t)
{
// CÁCH TỐI ƯU NHẤT
// nếu node cha mà không tồn cây con phải - thì node cha này chính là node ngoài cùng nhất của cây con phải - cũng chính là node có giá trị lớn nhất
if (t->pRight == NULL)
{
return t->data;
}
return TimMax(t->pRight); // duyệt đến node cuối cùng nhất bên cây con phải ==> để tìm giá trị lớn nhất
}2. Tìm giá trị MIN trong cây nhị phần tìm kiếm
Tương tự như tìm giá trị MAX trong cây nhị phân tìm kiếm, việc tìm giá trị MIN chỉ đơn giản là ta duyệt sang cây con trái, vì cây con trái luôn chứa giá trị nhỏ hơn Node cha. Như mình đã nói ở trên thì Node ngoài cùng bên trái luôn luôn là Node nhỏ nhất, vậy nên chỉ cần duyệt sang trái đến Node cuối cùng nhất thì đó chính là giá trị MIN.
//hàm tìm giá trị MIN
int TimMin(TREE t)
{
// CÁCH TỐI ƯU NHẤT
// nếu node cha mà không tồn cây con trái - thì node cha này chính là node ngoài cùng nhất của cây con trái - cũng chính là node có giá trị nhỏ nhất
if (t->pLeft == NULL)
{
return t->data;
}
return TimMin(t->pLeft); // duyệt đến node cuối cùng nhất bên cây con trái ==> để tìm giá trị nhỏ nhất
}3. Ví dụ: Tìm giá trị MAX, MIN trong cây nhị phân tìm kiếm
Trong ví dụ này mình sẽ thực hiện nhập vào một dãy các số nguyên sau đó in ra số có giá trị lớn nhất và nhỏ nhất. Để làm được bài toán này ta cần có các hàm sau:
- Cấu trúc dữ liệu của cây và Node.
- Hàm thêm Node vào cây.
- Hàm duyệt cây (chỉ cần một trong 6 hàm duyệt).
- Hàm tìm MAX.
- Hàm tìm MIN.
- Hàm menu để hiển thị.
Full code
#include<iostream>
using namespace std;
// khai báo cấu trúc 1 cái node trong cây nhị phân tìm kiếm
struct node
{
int data; // dữ liệu chứa trong 1 cái node
struct node *pLeft; // con trỏ liên kết với cái node bên trái <=> cây con trái
struct node *pRight; // con trỏ liên kết với cái node bên phải <=> cây con phải
};
typedef struct node NODE;
typedef NODE* TREE;
// hàm khởi tạo cây nhị phân tìm kiếm
void KhoiTaoCay(TREE &t)
{
t = NULL;
}
// hàm thêm 1 cái phần tử vào cây
void ThemNodeVaoCay(TREE &t, int x)
{
// nếu cây rỗng
if (t == NULL)
{
NODE *p = new NODE;
p->data = x;
p->pLeft = NULL;
p->pRight = NULL;
t = p;
}
else
{
// nếu phần tử thêm vào mà nhỏ hơn nút gốc thì sẽ duyệt qua bên trái
if (x < t->data)
{
ThemNodeVaoCay(t->pLeft, x);
}
else if (x > t->data)
{
ThemNodeVaoCay(t->pRight, x);
}
}
}
// hàm xuất phần tử trong cây nhị phân tìm kiếm
void NLR(TREE t)
{
if (t != NULL)
{
// xử lí
cout << t->data << " ";
NLR(t->pLeft);
NLR(t->pRight);
}
}
//Hàm tìm giá trị MAX
//------cách 1------------
// int MAX = INT_MIN; // gán cho biến MAX là giá trị nhỏ nhất của kiểu integer
// //// hàm tìm phần tử lớn nhất trong cây
// void TimMax(TREE t)
// {
// if (t != NULL)
// {
// // xử lí
// if (MAX < t->data)
// {
// MAX = t->data; // cập nhật lại giá trị cho biến MAX
// }
// TimMax(t->pLeft);
// TimMax(t->pRight);
// }
// }
int TimMax(TREE t)
{
// CÁCH TỐI ƯU NHẤT
// nếu node cha mà không tồn cây con phải - thì node cha này chính là node ngoài cùng nhất của cây con phải - cũng chính là node có giá trị lớn nhất
if (t->pRight == NULL)
{
return t->data;
}
return TimMax(t->pRight); // duyệt đến node cuối cùng nhất bên cây con phải ==> để tìm giá trị lớn nhất
}
//hàm tìm giá trị MIN
int TimMin(TREE t)
{
// CÁCH TỐI ƯU NHẤT
// nếu node cha mà không tồn cây con trái - thì node cha này chính là node ngoài cùng nhất của cây con trái - cũng chính là node có giá trị nhỏ nhất
if (t->pLeft == NULL)
{
return t->data;
}
return TimMin(t->pLeft); // duyệt đến node cuối cùng nhất bên cây con trái ==> để tìm giá trị nhỏ nhất
}
// hàm nhập cây nhị phân tìm kiếm
void Menu(TREE &t)
{
int luachon;
while(true)
{
cout << "
============ MENU ============";
cout << "
1. Nhập phần tử cho cây";
cout << "
2. Duyệt cây";
cout << "
3. Giá trị MAX";
cout << "
4. Giá trị MIN";
cout << "
0. Thoát";
cout << "
============= END =============";
cout << "
Nhập lựa chọn của bạn: ";
cin >> luachon;
if (luachon == 1)
{
int x;
cout << "
Nhập giá trị: ";
cin >> x;
ThemNodeVaoCay(t, x);
}
else if (luachon == 2)
{
cout << "
Cây nhị phân tìm kiếm
";
NLR(t);
}
else if (luachon == 3)
{
cout << "
Giá trị MAX: "<<TimMax(t);
}
else if (luachon == 4)
{
cout << "
Giá trị MAX: "<<TimMin(t);
}
else
{
break;
}
}
}
int main()
{
TREE t;
KhoiTaoCay(t);
Menu(t);
cout<<"
---------------------------------
";
cout<<"Chương trình này được đăng tại Zaidap.com.net";
}Kết quả:
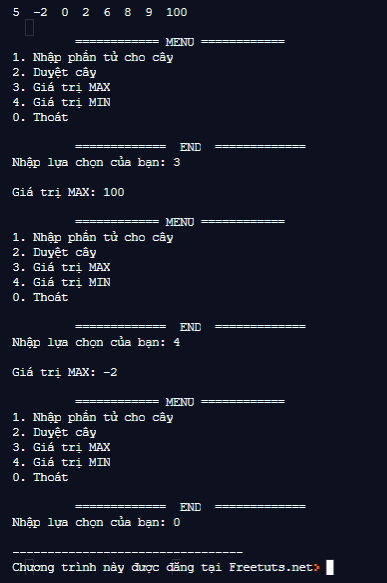
4. Kết luận
Như vậy là chúng ta tìm hiểu xong cách tìm giá trị MAX và MIN trong cây nhị phân tìm kiếm. Đây là một trong các thao tác đặc biệt trong cây nhị phân tìm kiếm, vì nó sinh ra để làm điều này. Trên đây là một số cách mà mình thực hiện, các bạn có thể thực hiện theo các cách khác nhau để tìm ta cách tối ưu nhất. Ở bài tiếp theo mình sẽ hướng dẫn các bạn cách xóa Node khỏi cây nhị phân tìm kiếm, các bạn nhớ chú ý theo dõi nhé !!!
