Ngăn xếp

Xin chào các bạn, như các bạn đã biết thì Cấu trúc dữ liệu & Giải thuật từ trước đến nay vẫn luôn là một phần quan trọng mà mỗi lập trình viên đều phải có. Việc hiểu và áp dụng được chúng sẽ giúp lập trình viên có khả năng giải quyết vấn đề một cách nhanh chóng và đơn giản. Vì vậy, trong bài hôm nay, mình sẽ trình bày với các bạn về chủ đề "Ngăn xếp - Stack".

1. Ngăn xếp là gì?

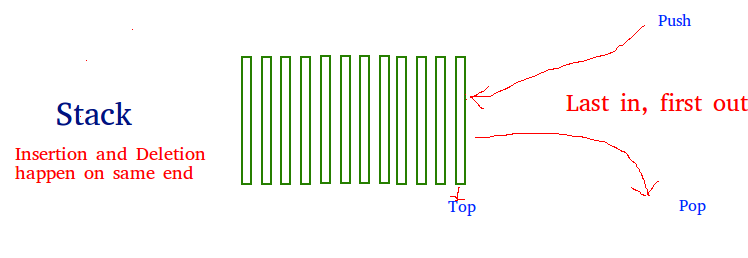
Theo ngành Khoa học Máy tính, Ngăn xếp(tiếng anh: Stack) là một loại cấu trúc dữ liệu trừu tượng để lưu trữ dữ liệu, hoạt động theo nguyên lý "Last-In-First-Out"(LIFO), được hiểu là "Vào sau ra trước".

Sở dĩ, loại cấu trúc dữ liệu này được đặt tên như vậy vì nó hoạt động giống như một ngăn xếp ở trong đời sống thực, chỉ cho phép các hoạt động tại vị trí trên cùng của ngăn xếp. Tại bất cứ thời điểm nào, chúng ta chỉ có thể truy cập phần tử trên cùng của Ngăn xếp.

Thật vậy, giả sử chúng ta có một chồng sách, chúng ta sẽ chỉ có thể đặt thêm một quyển sách cũng như chỉ lấy ra quyển sách ở trên cùng chồng sách. Hoặc nếu bạn muốn lấy một quyển sách bất kì, bạn sẽ phải lấy lần lượt từ quyển trên cùng, nếu không sẽ bị thay đổi cấu trúc của chồng sách.

2. Những phép toán của Ngăn xếp

Như đã nói ở phần trước, chúng ta sẽ dễ dàng nhận thấy được Ngăn xếp sẽ có hai thao tác chính, đó là Push và Pop:

• Push: Bổ sung một phần tử vào đỉnh của Ngăn xếp
• Pop: Giải phóng và trả về phần tử đang đứng ở đỉnh của Ngăn xếp.

Ngoài ra, Ngăn xếp cũng hỗ trợ một số các thao tác khác như:

• isEmpty(): Kiểm tra xem Ngăn xếp có rỗng không
• top(): Trả về giá trị của phần tử đứng đầu Ngăn xếp. Nếu Ngăn xếp không có phần tử nào, thao tác này sẽ bị lỗi.

Để hình dung một cách trực quan hơn, các bạn có thể nhìn vào hình vẽ minh họa dưới đây:

3. Ứng dụng của Ngăn xếp

Ngăn xếp là một trong những cấu trúc dữ liệu phổ biến, được áp dụng nhiều trong những thuật toán, mang ý nghĩa quan trọng trong ngành Khoa học Máy tính. Ở bài này, mình sẽ giới thiệu với các bạn 2 ứng dụng đơn giản của Ngăn xếp.

3.1. Tính toán các biểu thức đại số

Hiện nay, trên thị trường đã ra mắt nhiều loại máy tính cầm tay có hỗ trợ tính toán những biểu thức đại số phức tạp như Casio, Vinacal, ... Vậy làm thế nào máy tính có thể tính toán được những biểu thức ấy đúng theo quy tắc đại số. Cách làm đơn giản nhất đó là dùng Ngăn xếp.

Bài toán: Tính biểu thức: A = (1-2)x3+4x2

Giải thuật:

Sử dụng Ngăn xếp để lưu những số hạng.

Bước 1: Khử ngoặc, đưa biểu thức về dạng hậu tố: A = 1 2 - 3 x 4 2 x +

Bước 2: Duyệt biểu thức từ trái qua phải, đi qua mỗi phần tử:

• Nếu gặp một toán hạng (biến hoặc hằng), đặt (push)toán hạng đó vào Ngăn xếp
• Nếu gặp một toán tử, lấy (pop) hai phần tử trên đỉnh Ngăn xếp ra, thực hiện phép toán và đặt (push) lại kết quả vào Ngăn xếp.

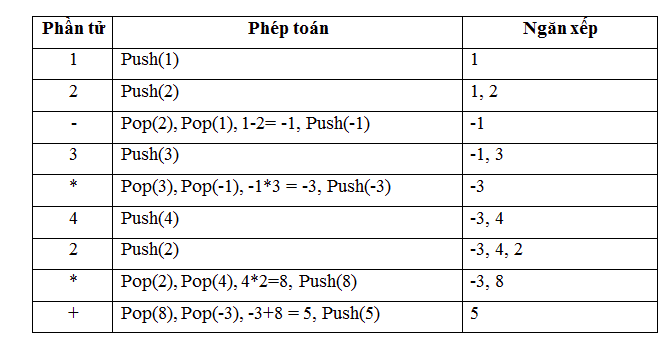
Sau khi duyệt xong, lấy giá trị ở đỉnh Ngăn xếp là kết quả của biểu thức.

Theo ví dụ, kết quả của biểu thức là 5, thử lại đúng luôn :3

3.2. Quản lý những thao tác back, forward trong các trình soạn thảo.

Trong tin học, những trình soạn thảo những văn bản thường hỗ trợ những thao tác quay lại(back) và chuyển tiếp(forward). Đó là một trong những ứng dụng điển hình của Ngăn xếp mà chúng ta thường tiếp xúc.

Bài toán: Xây dựng chương trình mô phỏng lại hệ thống back-forward của trình soạn thảo.

Giải thuật: Sử dụng 2 ngăn xếp để lưu trữ trạng thái của trình soạn thảo. Stack A dùng để lưu trữ hiện taị, Stack B dùng để lưu trữ những trạng thái đã được quay lại

• Mỗi khi trạng thái thay đổi, đẩy trạng thái vào ngăn xếp thứ nhất(stack A)
• BACK: Stack A sẽ pop phần tử Top, đồng thời đẩy luôn phần tử ấy sang Stack B
• FORWARD: Stack B sẽ pop phần tử Top, đồng thời đẩy vào Stack A
• Mọi thao tác, trạng thái hiển thị sẽ là trạng thái Top của Stack A(chữ màu đỏ).

3. Tổng kết

Như vậy, mình đã giới thiệu với các bạn về CTDL Ngăn xếp. Điểm cần lưu ý nhất đó là Ngăn xếp hoạt động theo nguyên lý "Last-In-First-Out". Trong quá trình tìm hiểu, sẽ không tránh khỏi những sai sót, nhầm lẫn, rất mong nhận được những góp ý từ các bạn độc giả. Xin chân thành cảm ơn.

4.