Quy hoạch động – một thuật toán thần thánh
Trong bài viết này, tôi sẽ giới thiệu với các bạn một thuật toán thần thánh: quy hoạch động. Nếu bạn tham gia các cuộc thi code, bạn nhất định phải biết thuật toán này. Gần một nửa các bài thi trong các cuộc thi code cần đến quy hoạch động. Tất nhiên, có những cách khác để giải bài ...

Trong bài viết này, tôi sẽ giới thiệu với các bạn một thuật toán thần thánh: quy hoạch động. Nếu bạn tham gia các cuộc thi code, bạn nhất định phải biết thuật toán này.
Gần một nửa các bài thi trong các cuộc thi code cần đến quy hoạch động. Tất nhiên, có những cách khác để giải bài toán đó. Nhưng vì các cuộc thi code đều có giới hạn về thời gian, cũng như bộ nhớ của chương trình, nên một thuật toán hiệu quả là cực kỳ cần thiết. Và trong những trường hợp như vậy, quy hoạch động là một trong những thuật toán xuất hiện nhiều nhất.
Thuật toán quy hoạch động được ưa chuộng bởi vì ban đầu, bài toán có muôn hình vạn trạng và bạn phải suy nghĩ rất nhiều mới tìm ra được lời giải. Không có một công thức chuẩn mực nào áp dụng được cho mọi bài toán. Bởi vì sự phổ biến của nó, bạn bắt buộc phải cực kỳ thuần thục thuật toán này nếu muốn có kết quả tốt trong các cuộc thi.
Cách hiệu quả nhất để tìm hiểu một thuật toán là xem xét những ví dụ cụ thể. Trong bài viết này, tôi sẽ giới thiệu vài ví dụ trong phần sau. Có thể nó chưa đầy đủ, bạn có thể đọc thêm ở các bài viết khác. Giới thiệu với các bạn một tài liệu rất hay: Dynamic Programming: From novice to advanced
Khi nào thì dùng quy hoạch động
Khi nào thì chúng ta cần đến quy hoạch động? Đó là một câu hỏi rất khó trả lời. Không có một công thức nào cho các bài toán như vậy.
Tuy nhiên, có một số tính chất của bài toán mà bạn có thể nghĩ đến quy hoạch động. Dưới đây là hai tính chất nổi bật nhất trong số chúng:
- Bài toán có các bài toán con gối nhau
- Bài toán có cấu trúc con tối ưu
Thường thì một bài toán có đủ cả hai tính chất này, chúng ta có thể dùng quy hoạch động được. Một câu hỏi rất thú vị là không dùng quy hoạch động có được không? Câu trả lời là có, nhưng nếu bạn đi thi code, bạn trượt là cái chắc. Để hiểu rõ hơn, chúng ta sẽ tìm hiểu từng tính chất một trong những phần dưới đây
Bài toán con gối nhau
Tương tự như thuật toán chia để trị, quy hoạch động cũng chia bài toán lớn thành các bài toán con nhỏ hơn. Quy hoạch động được sử dụng khi các bài toán con này được gọi đi gọi lại. Phương pháp quy hoạch động sẽ lưu kết quả của bài toán con này, và khi được gọi, nó sẽ không cần phải tính lại, do đó làm giảm thời gian tính toán.
Quy hoạch động sẽ không thể áp dụng được (hoặc nói đúng hơn là áp dụng cũng không có tác dụng gì) khi các bài toán con không gối nhau. Ví dụ với thuật toán tìm kiếm nhị phân, quy hoạch động cũng không thể tối ưu được gì cả, bởi vì mỗi khi chia nhỏ bài toán lớn thành các bài toán con, mỗi bài toán cũng chỉ cần giải một lần mà không bao giờ được gọi lại.
Một ví dụ rất điển hình của bài toán con gối nhau là bài toán tính số Fibonacci. Bài toán quá nổi tiếng rồi, chúng ta có thể tính toán số Fibonacci theo đúng công thức như sau:
|
1 2 3 4 5 6 |
def fib(n): if n <= 1: return n return fib(n -1) + fib(n - 2) |
Nếu tính toán như trên, chúng ta rất nhiều bài toán con sẽ được tính đi tính lại, điển hình là các số fib(0) và fib(1).
Và quy hoạch động chính là một trong số những phương pháp có thể giúp chúng ta tối ưu hóa quá trình tính toán này. Mỗi bài toán con (số fib) sẽ được lưu lại trước khi tính những bài toán con lớn hơn. Nhờ đó, mà việc tính toán giảm đi đáng kể, mỗi bài toán con chỉ cần tính đúng một lần.
Một ví dụ quy hoạch động với bài toán này như sau:
|
1 2 3 4 5 6 7 8 |
def fib(n): dp = [0] * (n + 1) dp[1] = 1 for i in range(2, n + 1): dp[i] = dp[i - 1] + dp[i - 2] return dp[n] |
Qua ví dụ trên, bạn đã thấy được sức mạnh vượt trội của quy hoạch động chưa? Đó cũng chính là lý do mà nó rất được ưa chuộng trong các cuộc thi lập trình, khi mà thời gian và bộ nhớ đều là hữu hạn (và thường khá nhỏ).
Cấu trúc con tối ưu
Cấu trúc con tối ưu là một tính chất là lời giải của bài toán lớn sẽ là tập hợp lời giải từ các bài toán nhỏ hơn.
Mình lấy một ví dụ cho dễ hiểu:
Trong bài toán tìm đường đi ngắn nhất trong đồ thị, nếu một node x nằm trên đường đi ngắn nhất giữa hai node u, v thì đường đi ngắn nhất từ u đến v sẽ là tổng hợp của đường đi ngắn nhất từ u đến x và đường đi ngắn nhất từ x đến v. Môt số thuật toán tìm đường trên đồ thị (nổi tiếng nhất có lẽ là Dijkstra) đều dựa trên tính chất này, và nó cũng áp dụng quy hoạch động.
Tính chất cấu trúc con tối ưu rất quan trọng. Nó cho phép chúng ta giải bài toán lớn dựa vào các bài toán con đã giải được. Nếu không có tính chất này, chúng ta không thể áp dụng quy hoạch động được.
Không phải bài toán nào cũng có tính chất cấu trúc con tối ưu này. Ví dụ với đồ thị sau:
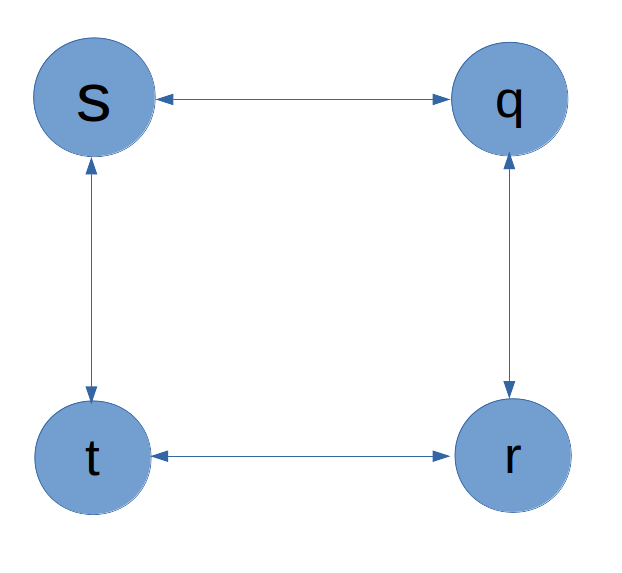
Đường đi dài nhất từ q -> t sẽ là q -> r -> t hoặc q -> s -> t. Nhưng không giống như bài toán tìm đường đi ngắn nhất, đường đi dài nhất không phải là tổ hợp của những đường đi thành phần, do đó, bài toán này không có cấu trúc con tối ưu.
Ví dụ, đường q -> r -> t không phải là tổ hợp của đường đi dài nhất từ q -> r và đường đi dài nhất từ r -> t. Bởi vì, đường đi dài nhất q -> r phải là q -> s -> t -> r và đường đi dài nhất từ r -> t phải là r -> q -> s -> t.
Một số bài toán quy hoạch động
Trong phần này, chúng ta sẽ làm quen với quy hoạch động thông qua một số ví dụ cụ thể. Chúng ta sẽ xem xét cách quy hoạch động được áp dụng vào các bài toán cụ thể như thế nào, đồng thời qua đó, chúng ta sẽ hiểu hơn về các tính chất ở phần trước.
Ví dụ 1: Bài toán kinh điển với đồng xu
Đây là một ví dụ rất kinh điển khi học về quy hoạch động. Có thể có nhiều cách phát biểu khác nhau nhưng về cơ bản, nội dung của nó sẽ tương tự như sau.
Giả sử chúng ta có n đồng xu nặng lần lượt là W1, W2, ..., Wn, và bài toán đặt ra là tìm số lượng đồng xu nhỏ nhất để tổng khối lượng của chúng là một giá trị S. Tất nhiên, số lượng đồng xu là không giới hạn.
Với bài toán này, chúng ta cần xây dựng và giải các bài toán con gối nhau. Với ví dụ của chúng ta, mỗi bài toán con dp(P) với P <= S là bài toán tìm số đồng xu nhỏ nhất để khối lượng của chúng là P. và dp(P) = k chính là số lượng đồng xu nhỏ nhất đó.
Chúng ta sẽ áp dụng phương pháp quy hoạch động bằng cách bắt đầu từ bài toán con dp(0) sau đó tiếp tục với các bài toán con lớn hơn. Lời giải của các bài toán con sẽ được xây dựng lần lượt cho đến chúng ta xây dựng đến bài toán dp(S) và đó chính là kết quả của bài toán lớn. Một điều cần lưu ý với kỹ thuật này là bài toán con tiếp theo sẽ không thể giải được nếu chúng ta chưa giải bài toán con trước đó.
Cuối cùng là phần khó nhất của mọi bài toán quy hoạch động, đó là trả lời câu hỏi: cấu trúc con tối ưu của bài toán này ở đâu. Hay nói một cách khác, làm thế nào để từ những bài toán nhỏ hơn có thể tổ hợp ra lời giải cho bài toán lớn. Với vị dụ kinh điển này, mọi thứ sẽ tương đối đơn giản, nhưng với những bài toán phức tạp hơn, chúng ta cần suy nghĩ và tính toán nhiều hơn.
Quay trở lại với bài toán của chúng ta. Giả sử P là tổng khối lượng của các đồng xu nặng lần lượt là V1, V2, ..., Vj. Để có được khối lượng P, chúng ta cần thêm vài đúng 1 đồng xu nặng U vào khối lượng Q sao cho Q + U = P. Tất nhiên, bài toán con dp(Q) chúng ta đã có lời giải nên chúng ta sẽ biết được cần bao nhiêu đồng xu cho dp(P). Và vì có nhiều đồng xu U (nhiều nhưng hữu hạn) nên chúng ta có thể cần đến nhiều bài toán con trước đó, và dp(p) là giá trị nhỏ nhất sau khi tổng hợp những bài toán con đó.
Ví dụ với n = 3, S = 11, W = [1, 3, 5].
- Bắt đầu với bài toán con 0 ta có dp(0) = 0
- Với bài toán con 1, có 1 đồng xu (nặng 1) có thể thêm vào từ 0 đồng xu nào cả. Vậy dp(1) = dp(0) + 1 = 1.
- Với bài toán con 2, cũng chỉ có 1 đồng xu (nặng 1) có thể thêm vào từ 1 đồng xu. Vậy dp(2) = dp(1) + 1 = 2.
- Với bài toán con 3, chúng ta có thể thêm 1 đồng xu 3 vào 0 đồng xu hoặc thêm 1 đồng xu 1 vào 2 đồng xu. Rõ ràng là cách đầu tiên cho kết quả nhỏ hơn. Vậy dp(3) = min(dp(2) + 1, dp(0) + 1) = min(3, 1) = 1
- …
- Cứ tiếp tục như vậy cho đến bài toán S chính là đáp án chúng ta cần tìm.
Về mặt cài đặt, quy hoạch động thường lưu kết quả vào một mảng. Trong ví dụ của chúng ta, mảng dp[0..S] sẽ lưu kết quả cho từng bài toán con. Nói cách khác, dp[P] = k nghĩa là cần ít nhất k đồng xu để có khối lượng là P Toàn bộ mảng này sẽ được tính bằng vòng lặp. Đoạn code sau mô tả toàn bộ quá trình này.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
n, S = map(int, input().split()) w = list(map(int, input().split())) dp = [0] * (S + 1) dp[0] = 0 for P in range(1, S + 1): dp[P] = min(dp[P - x] for x in w if x <= P) + 1 print(dp) print(dp[S]) # Nếu đầu vào như sau: n = 3, S = 11, w = [1, 3, 5] # Thì bảng lời giải cho các bài toán con sẽ lần lượt như sau: # P = 0 |1 |2 |3 |4 |5 |6 |7 |8 |9 |10|11 # ------+--+--+--+--+--+--+--+--+--+--+-- # k = 0 |1 |2 |1 |2 |1 |2 |3 |2 |3 |2 |3 |
Ví dụ 2: Xâu con chung dài nhất (LCS)
Thêm một ví dụ nữa cho dễ, cũng là một bài toán rất nổi tiếng.
Cho hai xâu ký tự. Tìm độ dài xâu con chung nhỏ nhất giữa chúng. Ví dụ với 2 xâu “quetzalcoatl” và “tezcatlipoca” thì xâu con chung dài nhất sẽ là “ezaloa” với độ dài 6.
Với bài toán này, chúng ta sẽ lần lượt giải các bài toán con như sau:
Lấy i ký tự đầu tiên từ xâu thứ nhất và j ký tự đầu tiên từ xâu thứ hai và tìm độ dài xâu chung dài nhất giữa 2 xâu con được lấy ra đó. Dễ dàng thấy được rằng, lời giải của mỗi bài toán con sẽ phụ thuộc vào i và j, dp(i, j). Và bài toán lớn sẽ được giải bằng cách lần lượt giải các bài toán con lần lượt từ dp(0, 0) và tăng dần độ dài xâu được lấy ra cho đến khi chúng ta lấy ra toàn bộ xâu của đề bài.
Chúng ta hãy bắt đầu lần lượt các bài toán con. Đương nhiên, nếu một trong hai xâu là rỗng thì xâu con chung của chúng cũng rỗng. Vậy dp(0, j) = dp(i, 0) = 0. Nếu cả i và j đều dương, chúng ta cần suy xét một vài trường hợp.
- Nếu ký tự cuối cùng của xâu thứ nhất không có mặt trong xâu con chung dài nhất, nó có thể bị bỏ qua mà không ảnh hưởng gì đến kết quả. Công thức ở đây sẽ là dp(i, j) = dp(i - 1, j).
- Tương tự như trường hợp trên, ký tự cuối cùng của xâu thứ hai không ảnh hưởng đến kết quả thì dp(i, j) = dp(i, j - 1).
- Trường hợp cuối cùng, nếu hai ký tự cuối cùng của hai xâu x1, x2 đều có mặt trong xâu con chung dài nhất. Dĩ nhiên là hai ký tự này phải là một thì điều này mới xảy ra, tức là x1 == x2. Trong trường hợp này, khi xoá đi bất cứ một ký tự nào trong hai ký tự đó đều khiến xâu con chung dài nhất ngắn đi 1 ký tự. Vậy rõ ràng là dp(i, j) = dp(i - 1, j - 1) + 1.
Trong cả ba trường hợp trên, chúng ta phải chọn ra trường hợp nào cho kết quả là xâu con chung dài nhất (với bài toán này thì chỉ cần đưa ra độ dài đó là đủ).
Về mặt cài đặt, dp sẽ được lưu trong mảng hai chiều. Kết quả của mảng này sẽ được tính toán thông qua vòng lặp hai lớp. Lưu ý rằng, chúng ta cần thực hiện vòng lặp sao cho chúng ta sẽ giải lần lượt từng bài toán con một, theo thứ tự từ nhỏ đến lớn. Bởi vì mỗi bài toán con dp(i, j) đều phụ thuộc vào các bài toán con trước đó dp(i - 1, j), dp(i, j - 1), dp(i - 1, j - 1).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
n1, n2 = map(int, input().split()) s1, s2 = input().split() t = [[0] * (len(s2) + 1) for _ in range(len(s1) + 1)] for i, x1 in enumerate(s1, 1): for j, x2 in enumerate(s2, 1): if x1 == x2: t[i][j] = t[i - 1][j - 1] + 1 else: t[i][j] = max(t[i][j - 1], t[i - 1][j]) print(t[-1][-1]) # Kết quả khi giải các bài toán con như bảng sau: # # S| t e z c a t l i p o c a # T ji| 0 1 2 3 4 5 6 7 8 9 10 11 12 # ----+-------------------------------------- # 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 # q 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0 # u 2 | 0 0 0 0 0 0 0 0 0 0 0 0 0 # e 3 | 0 0 1 1 1 1 1 1 1 1 1 1 1 # t 4 | 0 1 1 1 1 1 2 2 2 2 2 2 2 # z 5 | 0 1 1 2 2 2 2 2 2 2 2 2 2 # a 6 | 0 1 1 2 2 3 3 3 3 3 3 3 3 # l 7 | 0 1 1 2 2 3 3 4 4 4 4 4 4 # c 8 | 0 1 1 2 3 3 3 4 4 4 4 5 5 # o 9 | 0 1 1 2 3 3 3 4 4 4 5 5 5 # a 10| 0 1 1 2 3 4 4 4 4 4 5 5 6 # t 11| 0 1 1 2 3 4 5 5 5 5 5 5 6 # l 12| 0 1 1 2 3 4 5 6 6 6 6 6 6 |
Quy hoạch động vs. Memoization
Có một kỹ thuật khác gọi là “memoization” cũng có cách tiếp cận tương tự với quy hoạch động. Cả quy hoạch động và memoization đều dùng để tối ưu các vòng lặp mà có tính toán tượng tự nhau, trong đó kết quả của phép tính lớn hơn sẽ cần được tính toán dựa vào kết quả của phép tính nhỏ hơn. Memoization thường được sử dụng trong các phép tính đệ quy khi mà một tính toán bị lặp đi lặp lại nhiều lần. Nó sẽ lưu một bảng các giá trị tính được, mỗi khi có tính toán cần thực hiện, chúng ta sẽ tra bảng đó trước. Nếu bảng đã có kết quả rồi, chúng ta chỉ cần lấy ra là xong, nếu chưa, chúng ta sẽ tính toán như thường và tiếp tục lưu vào bảng.
Memoization không phải là một thuật toán theo đúng nghĩa, nó là một kỹ thuật được sử dụng trong lập trình thì đúng hơn. Để hiểu rõ hơn về kỹ thuật này, mình xin lấy ví dụ ngay với bài toán Fibonacci. Chúng ta sẽ sử dụng memoization như sau:
|
1 2 3 4 5 6 7 |
look_up = {0: 1, 1: 1} def fib(n): if look_up.get(n) is None: look_up[n] = fib(n - 1) + fib(n - 2) return look_up[n] |
Sự khác biệt chủ yếu là quy hoạch động sẽ thực hiện việc tính toán theo một thứ tự định trước, trong khi memoization duyệt theo chiều sâu. Quy hoạch động không bao giờ tính toán một bài toán con hai lần, tương đối giống với các phép tính đệ quy với memoization. Tuy nhiên memoization thì không bao giờ tính toán những phép tính thừa trong khi quy hoạch động sẽ cần tất cả mọi bài toán con. Đây là một phương pháp khá hay, nó chỉ tính toán những gì cần thiết và lưu kết quả này lại để sau này dùng lại khi nào được gọi mà không cần tính toán nữa.
Dưới đây là một số ưu, nhược điểm của memoization khi so sánh với quy hoạch động:
** Ưu điểm **
- Dễ code hơn
- Không yêu cầu thứ tự thực hiện tính toán
- Chỉ tính toán những gì cần thiết
** Nhược điểm **
- Chỉ có một kiểu duyệt duy nhất
- Thường chậm hơn quy hoạch động.
Các dạng toán quy hoạch động
Phần lớn các bài toán quy hoạch động có thể chia làm hai loại: bài toán cần quy hoạch động để tối ưu và bài toán quy tổ hợp. Trong những phần dưới đây, chúng ta sẽ xem xét từng loại bài toán này.
Bài toán tối ưu
Bài toán tối ưu yêu cầu chúng ta phải tìm đáp án tốt nhất từ mục tiêu của bài toán. Cả hai ví dụ mình đưa ra ở trên đều thuộc loại bài toán này (một bài tìm số đồng xu ít nhất, một bài tìm xâu con dài nhất). Mối liên hệ của các bài toán con thuộc dạng này có công thức chúng là dp[s] = min(F1(dp[i], dp[j], ..., dp[k]), F2(dp[u], dp[v], ..., dp[w]), ..., Fl(dp[q], dp[p], ..., dp[z])), trong đó dp mảng lưu kết quả của các bài toán con đó.
Mỗi bài toán được giải dựa trên bài toán đã được giải trước đó. Đây chính là tính chất cấu trúc con tối ưu của mỗi bài toán. Với bài toán đồng xu, mỗi bài toán mới đều được giải bằng cách thêm đúng 1 đồng xu vào kết quả từ trước đó. Kết quả cuối cùng là kết quả tốt nhất thu được từ nhiều cách thêm đồng xu với khối lượng khác nhau.
Trước khi tính toán, mảng chứa kết quả có thể được điền đầy một giá trị trung tính nào đó. Giá trị trung tính có nghĩa là giá trị đó sẽ không bao giờ là đáp án cho bất kỳ bài toán con nào. Ví dụ khi cần tìm ra số đồng xu nhỏ nhất, chúng ta có thể điền mảng này bằng số dương lớn nhất, mọi tính toán tiếp theo sẽ cho ra một kết quả nhỏ hơn nhiều. Nếu không ra kết quả nào khác, chúng ta có thể coi như là không có một đáp án nào cho bài toán con đó.
Bài toán tổ hợp
Bài toán tổ hợp thường yêu cầu chúng ta tìm ra số cách khác nhau để thực hiện một việc gì đó. Nhiều bài thi code thường có kết quả rất lớn và họ yêu cầu chúng ta đưa đáp án dạng modulo của 10000007. Trong dạng bài toán này, công thức khi xây dựng các bài toán con sẽ là R[s] = F1(R[i], R[j], ..., R[k]) + F2(R[u], R[v], ..., R[w]) + ... + Fl(R[q], R[p], ..., R[z]). Sự khác biệt cơ bản của dạng bài toán này với dạng bài toán tối ưu là ở chỗ chúng ta cần tính tổng thay vì tìm số lớn nhất hoặc nhỏ nhất.
Trong mọi bài toán quy hoạch động, tính chất cấu trúc con tối ưu luôn là quan trọng nhất và cũng là tính chất khó đảm bảo nhất. Nếu cấu trúc con không được tối ưu, chúng ta sẽ tính toán theo một phương thức sai lầm và đương nhiên, kết quả thu được cũng không chính xác.
Với phần lớn các bài toán quy hoạch động, việc chia các bài toán con gối nhau khá dễ dàng trong khi đảm bảo cấu trúc con tối ưu thì khó hơn nhiều.
Mình sẽ đưa ra hai ví dụ tương tự nhau cho các bạn hiểu rõ hơn về những khó khăn để đảm bảo tính chất này.
Vẫn với bài toán đồng xu, chúng ta sẽ thay đổi một chút để có bài toán tổ hợp như sau:
Tìm số cách khác nhau để chọn ra các đồng xu sao cho tổng khối lượng của chúng là S.
Các bài toán con sẽ tương tự như trước: dp(P) = k là số cách khác nhau để chọn ra các đồng xu có tổng khối lượng là P. Công thức đệ quy trong trường hợp này sẽ biến đổi theo bài toán như sau:
|
1 2 3 4 5 6 7 8 9 10 11 |
# Công thức đệ quy cho bài toán quy hoạch động # {dp[0] = 1; # {dp[P] = sum(dp[P-Wi]); (for Wi <= P) # # Với đầu vào như sau: n = 3, S = 11, W = [1, 3, 5] # Mảng kết quả quy hoạch động sẽ là # P = 0 |1 |2 |3 |4 |5 |6 |7 |8 |9 |10|11 # ------+--+--+--+--+--+--+--+--+--+--+-- # k = 1 |1 |1 |2 |3 |5 |8 |12|19|30|47|74 |
Bài toán tổ hợp cũng có thể có một giá trị trung tính. Bởi vì bài toán tổ hợp thường tính tổng, giá trị trung tính sẽ là 0. Bài toán tổ hợp yêu cầu tìm số cách khác nhau để làm gì đó, do đó giá trị 0 sẽ không ảnh hưởng gì đến đáp án. Một điểm đặc biệt quan trọng trong bài toán tổ hợp này là mỗi cách chúng ta chỉ tính đúng một lần. Nói thì dễ nhưng nhiều khi trong thực hành chúng ta hay gặp sai sót ở chỗ cực kỳ quan trọng này.
Tiếp tục thay đổi thêm một chút, chúng ta sẽ có bài toán tổ hợp như sau:
Tìm số cách khác nhau để chọn ra các đồng xu sao cho tổng khối lượng của chúng là S. Với điều kiện, các cách lấy đồng xu là hoán vị của nhau không được coi là khác nhau.
Bài toán này khó hơn bài toán trước một chút. Nếu chúng vẫn chia các bài toán con như cũ thì không thể có được cấu trúc con tối ưu. Ví dụ, với các đồng xu 1, 3, 5 thì (1, 3) và (3, 1) đều cho kết quả là 4 nhưng chỉ được coi là 1 cách.
Với bài toán này, chúng ta sẽ chia bài toán lớn thành các bài toán con theo một cách tương đối khác. Chúng ta thấy rằng, kết quả (số cách chọn đồng xu) sẽ là tổng hợp của hai kết quả:
- Số cách lấy đồng xu từ n - 1 đồng xu đầu tiên, tức là chúng ta coi như không có đồng xu nặng nhất
- Số cách lấy đồng xu có chứa đồng xu nặng nhất.
Kết quả sẽ là tổng của hai kết quả trên. Các bạn thấy đó, với cách xây dựng bài toán con như thế này, chúng ta đã xây dựng các bài toán con gối nhau mà vẫn đảm bảo cấu trúc con tối ưu (kết quả bằng tổng của các bài toán con).
Nhân tiện, với cách chia bài toán như vậy, chúng ta có thể thu được lời giải bằng cách đệ quy đơn giản như sau:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
n, S = map(int, input().split()) w = list(map(int, input().split())) def count(arr, x): # Có 1 cách (lấy ra 0 đồng xu) cho tổng khối lượng bằng 0 if x == 0: return 1 # Không thể lấy được các đồng xu cho khối lượng âm if x < 0: return 0 # Không thể lấy nếu không có đồng xu nào if not arr and x >= 1: return 0 # Kết quả là tổ hợp các bài toán con return count(arr[:-1], x) + count(arr, x - arr[-1]) print(count(w, S)) |
Tuy nhiên, như mình đã nói ở phần trước, nếu bạn đang thi code, cách làm này sẽ không mang lại bất cứ hy vọng đạt giải nào, do nó cực kỳ mất thời gian và bộ nhớ. Tuy nhiên, chúng ta có thể áp dụng quy hoạch động cho bài toán này rất dễ dàng sau khi có được cấu trúc con tối ưu với các bài toán con gối nhau:
