12/08/2018, 16:14

Sử dụng hệ mờ giải bài toán tính thời gian bơm nước

Cho bể nước cao 10 m; hồ trên tầng thượng cao 2m; 1 máy bơm nước bơm từ bể vào hồ. Hỏi bơm bao lâu thì hồ đầy? biết bơm lâu mất 30 phút, bơm hơi lâu 20 phút và bơm vừa 15 phút. Cho giá trị nước ở bể ban đầu là y0= 1^m, giá trị ban đầu của hồ là x0 = 2^m. Hãy sử dụng hệ mờ để ước lượng thời gian ...

Cho bể nước cao 10 m; hồ trên tầng thượng cao 2m; 1 máy bơm nước bơm từ bể vào hồ. Hỏi bơm bao lâu thì hồ đầy? biết bơm lâu mất 30 phút, bơm hơi lâu 20 phút và bơm vừa 15 phút. Cho giá trị nước ở bể ban đầu là y0= 1^m, giá trị ban đầu của hồ là x0 = 2^m. Hãy sử dụng hệ mờ để ước lượng thời gian bơm bao lâu thì bể đầy?

Phân tích: Bài này trong thực tế sẽ không giải được vì vẫn thiếu nhiều sự kiện như không thể tính dung tích chứa nước của bể, của hồ; không cho công suất của máy bơm. Nhưng vẫn có thể phỏng đoán kết quả bằng suy diễn thông thường, đó là: . Đó là dùng hệ mờ để giải. Tuy nhiên, dùng hệ mờ chỉ tính được kết quả gần đúng không thể chính xác hoàn toàn.

1.Cơ sở lý thuyết

Tập mờ

Định nghĩa : Một tập mờ trong một vũ trụ luận U được đặc trưng bởi một hàm thành viên pA (x) có giá trị trong khoảng [0, 1]. Do đó, một tập mờ là một sự tổng quát của một tập cổ điển bằng cách cho phép các hàm thành viên để có bất kỳ giá trị trong khoảng [0, 1]. Nói cách khác, các hàm thành viên của một tập cổ điển chỉ có thể lấy hai giá trị không và một, trong khi hàm thành viên của một tập mờ là một hàm liên tục với phạm vi [0, 1].

Hàm thuộc về (hàm thành viên)

Có hai cách tiếp cận để xác định một hàm thành viên.

Phương pháp tiếp cận đầu tiên là sử dụng kiến thức của các chuyên gia của con người, đó là, yêu cầu các chuyên gia tên miền để xác định các hàm thành viên. Thông thường, phương pháp này chỉ có thể cung cấp cho một công thức của hàm thành viên; tinh chỉnh là cần thiết
Phương pháp thứ hai, sử dụng dữ liệu thu thập từ các cảm biến khác nhau để xác định các hàm thành viên. Trước tiên, xác định cấu trúc của các hàm thành viên và sau đó tinh chỉnh các thông số của các hàm thành viên dựa trên dữ liệu. Đặc điểm: Các hàm thành viên có 3 dạng:
Dạng tăng:
Dạng giảm:
Dạng vừa tăng vừa giảm:

Hệ mờ

Hệ thống mờ là những hệ thống dựa trên tri thức hay dựa trên quy luật mà trung tâm là là một cơ sở tri thức bao gồm cái gọi là mờ cấu trúc IF-THEN. Ví dụ IF “Trời mưa” THEN “đất ướt”. 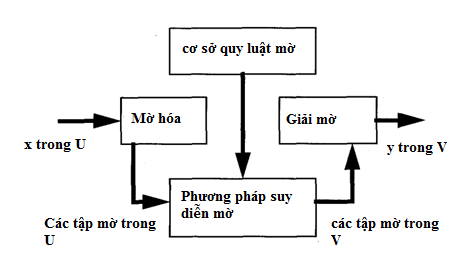Hệ mờ hoạt động như sau: Mờ hóa các biến vào: vì nhiều luật cho dưới dạng các biến ngôn ngữ với các từ thông thường. Như vậy với những giá trị quan sát được, đo được cụ thể, để có thể tham gia vào quá trình suy diễn thì cần thiết phải mờ hóa Có thể định nghĩa mờ hóa là ánh xạ từ không gian các giá trị quan sát được vào không gian các từ trên không gian nền cuả các biến ngôn ngữ. Áp dụng các toán tử mờ (AND, OR, NOT) cho các giả thiết của từng luật Giải mờ kết quả để tìm được một số rõ, một số cụ thể: Đây là khâu thực hiện quá trình xác định một giá trị rõ có thể chấp nhận được làm đầu ra của hàm thuộc của giá trị mờ đầu ra.

Các phép tính mờ

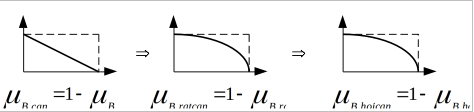
Sự bằng nhau, chứa nhau, bù, hợp, và giao của hai tập mờ A và B được định nghĩa như sau. Chúng ta nói A và B bằng nhau khi và chỉ khi µA (x) = µB (x) với mọi x U. Chúng ta nói B chứa A, ký hiệu là AB, khi và chỉ khi µA (x) ≤ µB (x) với mọi xU. Bù của A là một tập mờ phủ định A trong U mà hàm thành viên được định nghĩa là 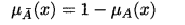Hợp của A và B là một tập mờ trong U, ký hiệu là AUB, trong đó hàm thành viên được xác định: 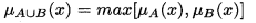Giao điểm của A và B là một tập mờ AB trong U với hàm thành viên: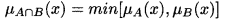

Mờ hóa

Được định nghĩa là sự ánh xạ từ các tập giá trị x thuộc U và là tập con của R thành tập các giá trị mờ A ở trong U. Nguyên tắc chung việc thực hiện mờ hóa:

Từ tập x giá trị đầu vào sẽ tạo ra tập giá trị mờ A với hàm thuộc có giá trị đủ rộng tại các điểm rõ x
Nếu có nhiễu ở đầu vào thì mờ hóa sẽ góp phần khử nhiễu
Việc mờ hóa phải làm đơn giản cho việc tính toán sau này Thông thường, có 3 phương pháp mờ hóa:
Mờ hóa đơn vị: là từ các điểm giá trị thực x thuộc U lấy giá trị đơn của tập mờ A
Mờ hóa Gaus: từ các điểm giá trị thực x thuộc U lấy giá trị đơn của tập mờ A thuộc hàm Gaus.
Mờ hóa hình tam giác: từ các điểm giá trị thực x thuộc U lấy giá trị đơn của tập mờ A thuộc hàm hình tam giác. Ta thấy rằng mờ hóa đơn vị tính toán về sau đơn giản hơn so với 2 cách còn lại nhưng nó lại không khử được nhiễu đầu vào. Mờ hóa Gaus và hình tam giác cho tính toán phức tạp hơn nhưng khử được nhiễu đầu vào.

Giải mờ

Có 3 điều cần lưu ý khi giải mờ

Tính hợp lý của kết quả: Điểm rõ y phải thuộc V là điểm đại diện cho kết quả của tập mờ B.
Việc tính toán đơn giản: Đây là điều quan trọng để tính toán nhanh vì các bộ điều khiển mờ thường làm việc trong thời gian thực.
Tính liên tục: mọi sự thay đổi nhỏ trong tập mờ B chỉ làm thay đổi nhỏ kết quả giải mờ. Có 3 phương pháp giải mờ: phương pháp cực đại, phương pháp tâm của trọng lực và phương pháp tìm tâm trung bình
Phương pháp cực đại
Phương pháp trọng tâm
Phương pháp trung bình tâm

2. Giải quyết bài toán

Bước 1: Xây dựng biến ngôn ngữ và các hàm thành viên (khâu mờ hóa)

Cho 1 bể nước cao 10m có 3 mức nước:
Một hồ nước cao 2m có 3 mức nước:
Một cái bơm có 3 trạng thái: Bước 2: Xây dựng hệ cơ sở trí thức. Từ kinh nghiệm (ý kiến của chuyên gia) ta có thể xây dựng được bảng như dưới đây.

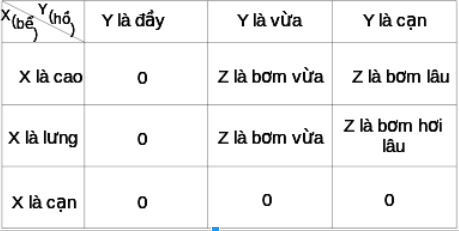
Bước 3: Viết luật. Từ bảng mô tả tri thức trên, có thể mô tả thành 4 luật như sau: Luật 1: IF(x là cao) ∧ (y là vừa) THEN (z là bơm vừa) Luật2: IF (x là lưng) ∧ (y là vừa) THEN (z là bơm vừa) Luật 3: IF (x là cao) ∧ (y là cạn) THEN (z là bơm lâu) Luật 4: IF (x là lưng) ∧ (y là cạn) THEN (z bơm hơi lâu)

Bước 4: Tính toán mờ (hay chính xác hơn suy diễn mờ) thuộc khối: động cơ suy diễn (Inference Engine: phần chính yếu của hệ mờ). Để thực hiện tính toán mờ bằng trực quan, chúng ta mô tả lời giải bằng phương pháp đồ thi hay ma trận (bảng) suy diễn. Trong ma trận (bảng) dưới đây, các dòng thể hiện các luật; các cột gồm hai phần: i) phần đầu vào phía bên trái mô tả đầu vào 1: biến x, đầu vào 2: biến y; ii) phần đầu ra y. 4.1. Phần chuẩn bị Vẽ đồ thị theo mô tả của luật. đưa các giá trị ban đầu là y0= 1^m, giá trị ban đầu của hồ là x0 = 2^m vào các cột tương ứng. Các giá trị đó cắt các đường đặc tính của các hàm thuộc về với các giá trị tương ứng. Tại các điểm cắt, kéo theo trục ngang; gạch chân phần diện tích mà đương kéo dài trục ngang với trục ngang tọa độ (xem hình dưới đây). 4.2. Phần suy diễn mờ.
Giả sử luật suy diễn được chọn là Suy diễn Mamdani. Trong bài toán này, các luật hợp thành của các luật mờ sử dụng toán tử AND. Và luật tính giá trị hàm thuộc về đầu ra là hàm MIN. Để thực hiện điều này trên đồ thị, thực hiện từng dòng (theo từng luật như sau: Từ các giá trị hàm thuộc của mỗi dòng, xét giá trị nào nhỏ nhất (MIN), chiếu sang kết quả đầu ra.cắt đường đặc trưng đầu ra của mỗi đường. Gạch chéo phần diện tích được bao của đầu ra như đã gạch chân ở đầu vào. Lặp lại cho hết các luật (các dòng trên biêu đồ ma trận).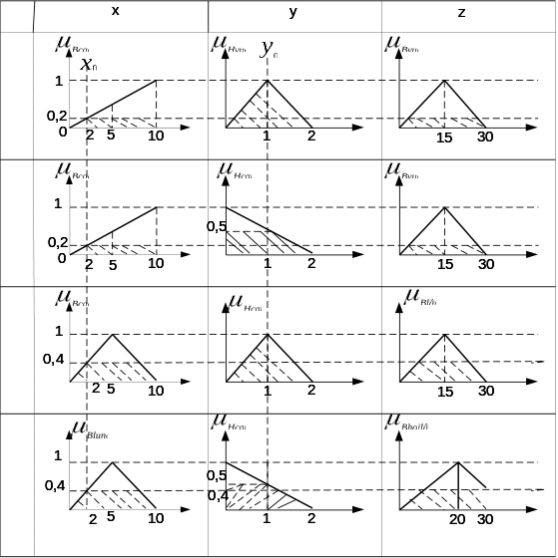

Bước 5: Giải mờ. Từ các kết quả ở bước B4, sử dụng một trong các phương pháp mờ hóa để tìm kết quả cuối cùng. Cho dù phương pháp này hay phương pháp khác, nguyên tắc chung của giải mờ được những nhà nghiên cứu sử dụng theo nguyên lý trung bình của các đầu ra. Để đơn giản trong minh họa và hiểu được nguyên tắc, nhưng không làm mất tính tổng quát, chúng ta sử dụng phương pháp tính toán trung bình theo các giá trị lớn nhất của các cận trái và cận phải; Đối với đầu ra của luật 1(dòng 1): ZMAX.1=6 (phút); ZMAX.2=30-6 (phút) ZTRUNG_BÌNH.1= (ZMAX.1+ ZMAX.2)/2= [6 phút +(30-6 phút]/2= 15 phút.