Support Vector Machine trong học máy - Một cái nhìn đơn giản hơn
Xin chào các bạn, nếu như các bạn có theo dõi các bài viết trước của mình về các mô hình hồi quy thì chúng ta có thể dễ dàng nhận thấy được sự đơn giản và dễ áp dụng của phương pháp hồi quy, nhất là trong các bài toán dự đoán (prediction). Tuy nhiên chính sự đơn giản đó của mô hình làm cho hiệu quả ...
Xin chào các bạn, nếu như các bạn có theo dõi các bài viết trước của mình về các mô hình hồi quy thì chúng ta có thể dễ dàng nhận thấy được sự đơn giản và dễ áp dụng của phương pháp hồi quy, nhất là trong các bài toán dự đoán (prediction). Tuy nhiên chính sự đơn giản đó của mô hình làm cho hiệu quả của thuật toán chưa thật sự được như mong muốn. Có rất nhiều phương pháp cho hiệu quả tốt hơn các phương pháp hồi quy, và một trong số đó là Support Vector Machine (SVM) mà mình sẽ giới thiệu thật kĩ trong bài viết này. Tuy nhiên, để tránh nhàm chán với những yếu tố học thuật trong bài này chúng ta sẽ tìm hiểu SVM theo cách mà người ta vẫn hay kiểm tra học sinh tiểu học theo dạng cô hỏi - trò đáp. OK chúng ta bắt đầu thôi
Khái niệm - SVM là gì

Nhìn hình ảnh chúng ta cũng có thể đoán được mục đích của nó đúng không. SVM sử dụng để tìm ra một siêu phẳng (hyperplane) - chính là cái đường cong cong như hình trên đó. Nhưng thử tưởng tượng trong không gian nhiều chiều hơn chẳng hạn, nó có thể là một mặt cầu, mặt bầu dục... Tóm lại mục đích của cái siêu phẳng đó là phân tách tập dữ liệu thành hai phần riêng biệt - tư tưởng của bài toán phân lớp. Ví dụ như ảnh trên, chúng ta có một mặt bàn đựng hai loại quả lê và táo. Siêu phẳng phân tách đống quả này thành hai lớp, bản chất là đi tìm một hàm toán học phụ thuộc tọa độ của một quả trên mặt bàn. Có nghĩa là khi nhét một quả mới vào trên mặt bàn, dựa vào tọa độ của nó ta có thể biết được nó là quả táo hay quả lê nhờ vào việc nó nằm bên phải hay bên trái của siêu phẳng. Có thể hiểu đơn giản như thế. Tuy nhiên các phần sau bắt đầu phức tạp rồi đấy, các bạn chuẩn bị tinh thần nha.
Ánh xạ tập dữ liệu vào không gian nhiều chiều
Trở lại với ví dụ trên của chúng ta, nếu như các quả táo và lê không năm quá đan xen nhạu thì chúng ta hoàn toàn có thể dùng một cái que (siêu phẳng) phân tách chúng. Tuy nhiên, thực tế không phải đơn giản như thế, có nghĩa là các quả táo và quả lê nằm tại các vị trí rất lung tung trên mặt bàn và rất khó có thể tìm được một cái que như thế để phân tách giữa chúng. Vậy thì làm thế nào bây giờ??? Một cách giải quyết đó là vận dụng tư tưởng của trò chơi tung hứng. Giả sử chúng ta trong một cơn tức giận hất tung chiếc bạn đựng táo và lê lên trời, các quả táo và lê bay lơ lửng trên không trung. Lúc này chúng đã ở các vị trí khác nhau và chúng ta hoàn toàn có thể dùng một mặt cong tưởng tượng để phân tách giữa chúng. Ví dụ như mặt phẳng xanh bên đưới đây.
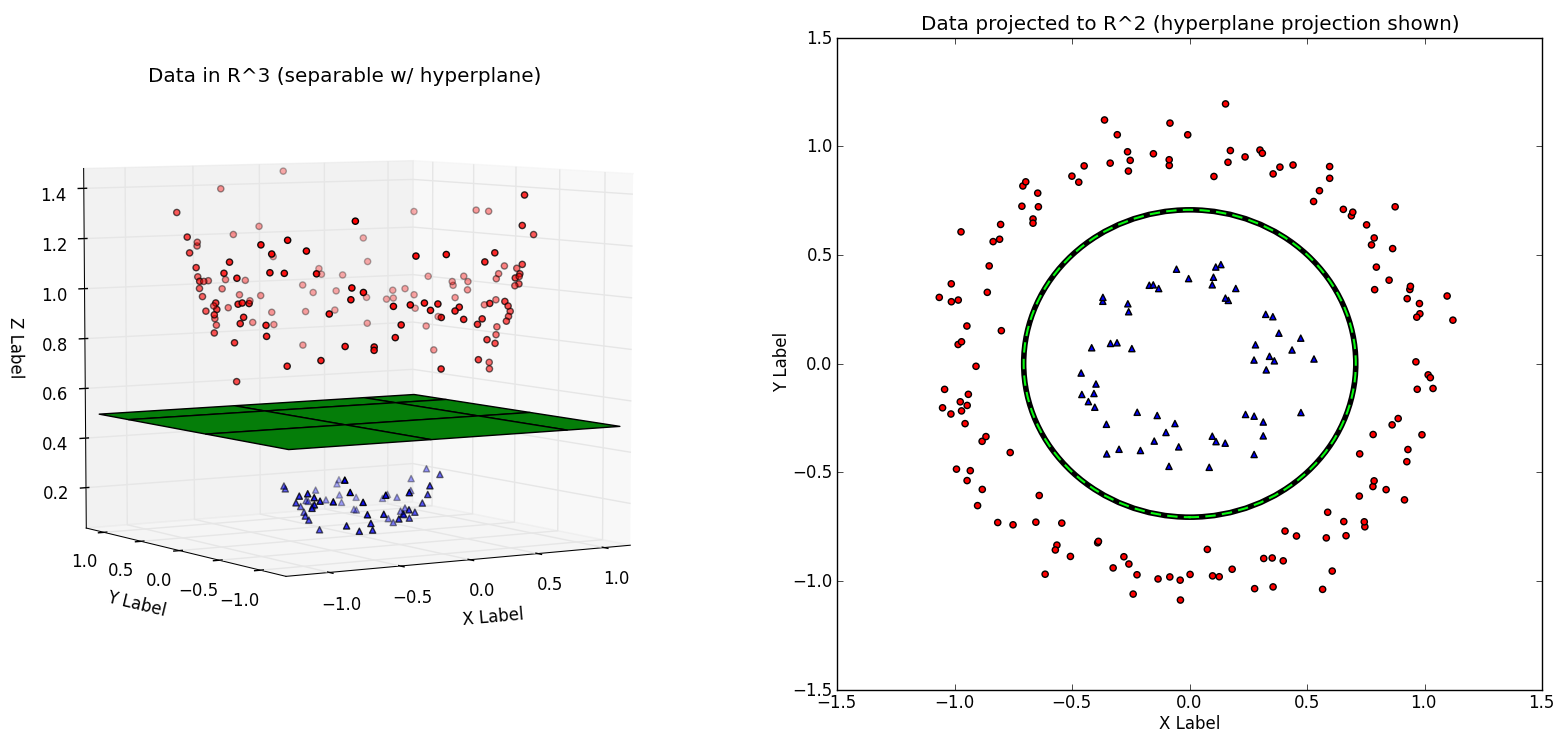
Các bạn sẽ nghĩ là có cái gì đó chém gió ở đây phải không? Không hề đâu, trò chơi tung hứng trong thực tế tương đương với việc chuyển đổi từ không gian hai chiều (mặt bàn) sang không gian nhiều chiều hơn (không trung). SVM thực hiện điều này một cách rất tự nhiên thông qua Kernel. Mình không hề chém gió chút nào đâu. Chúng ta cũng có thể hình dung dễ hơn việc tung bóng này của SVM thực hiện ra sao trong video dưới đây:
{@youtube: https://youtu.be/3liCbRZPrZA}
SVM thực hiện điều này như thế nào?
Như chúng ta đã thảo luận ở các phần trên, bản chất của phương pháp SVM là chuyển không gian dữ liệu ban đầu thành một không gian mới hữu hạn chiều mà ở đó cho khả năng phân lớp dễ dàng hơn. Một quả bất kì nằm trên mặt bàn sẽ được gắn với một tọa độ cụ thể. Ví dụ, quả táo nằm cách mép trái 2cm và cách mép dưới 5cm được thể hiện trên trục tọa độ (x, y) tương ứng là (2, 5). x và y chính là tọa độ trong không gian hai chiều của quả táo. Khi đưa lên chiều thứ 3 là z(x, y), ta có thể tính được tọa độ của z trong không gian 3 chiều dựa vào tọa độ x,y ban đầu. Điểm làm SVM hiệu quả hơn các phương pháp khác chính là việc sử dụng Kernel Method giúp cho SVM không còn bị giới hạn bởi việc phân lớp một cách tuyến tính, hay nói cách khác các siêu phẳng có thể được hình thành từ các hàm phi tuyến.
Margin trong SVM là gì?
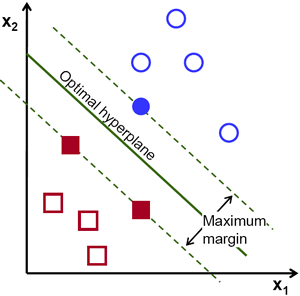
Margin là khoảng cách giữa siêu phẳng đến 2 điểm dữ liệu gần nhất tương ứng với các phân lớp. Trong ví dụ quả táo quả lê đặt trên mặt bán, margin chính là khoảng cách giữa cây que và hai quả táo và lê gần nó nhất.
Điều quan trọng ở đây đó là phương pháp SVM luôn cô gắng cực đại hóa margin này, từ đó thu được một siêu phẳng tạo khoảng cách xa nhất so với 2 quả táo và lê. Nhờ vậy, SVM có thể giảm thiểu việc phân lớp sai (misclassification) đối với điểm dữ liệu mới đưa vào.
Ưu điểm của SVM là gì?
Là một kĩ thuật phân lớp khá phổ biến, SVM thể hiện được nhiều ưu điểm trong số đó có việc tính toán hiệu quả trên các tập dữ liệu lớn. Có thể kể thêm một số ưu điểm của phương pháp này như:
- Xử lý trên không gian số chiều cao: SVM là một công cụ tính toán hiệu quả trong không gian chiều cao, trong đó đặc biệt áp dụng cho các bài toán phân loại văn bản và phân tích quan điểm nơi chiều có thể cực kỳ lớn
- Tiết kiệm bộ nhớ: Do chỉ có một tập hợp con của các điểm được sử dụng trong quá trình huấn luyện và ra quyết định thực tế cho các điểm dữ liệu mới nên chỉ có những điểm cần thiết mới được lưu trữ trong bộ nhớ khi ra quyết dịnh
- Tính linh hoạt - phân lớp thường là phi tuyến tính. Khả năng áp dụng Kernel mới cho phép linh động giữa các phương pháp tuyến tính và phi tuyến tính từ đó khiến cho hiệu suất phân loại lớn hơn.
Nhược điểm của SVM là gì?
- Bài toán số chiều cao: Trong trường hợp số lượng thuộc tính (p) của tập dữ liệu lớn hơn rất nhiều so với số lượng dữ liệu (n) thì SVM cho kết quả khá tồi
- Chưa thể hiện rõ tính xác suất: Việc phân lớp của SVM chỉ là việc cố gắng tách các đối tượng vào hai lớp được phân tách bởi siêu phẳng SVM. Điều này chưa giải thích được xác suất xuất hiện của một thành viên trong một nhóm là như thế nào. Tuy nhiên hiệu quả của việc phân lớp có thể được xác định dựa vào khái niệm margin từ điểm dữ liệu mới đến siêu phẳng phân lớp mà chúng ta đã bàn luận ở trên.
Kết luận
SVM là một phương pháp hiệu quả cho bài toán phân lớp dữ liệu. Nó là một công cụ đắc lực cho các bài toán về xử lý ảnh, phân loại văn bản, phân tích quan điểm. Một yếu tố làm nên hiệu quả của SVM đó là việc sử dụng Kernel function khiến cho các phương pháp chuyển không gian trở nên linh hoạt hơn.
Tham khảo
Support Vector Machine Tutorial
SVM Exercise
