[Thuật toán – Java] Chuyển biểu thức trung tố sang hậu tố – Java – converts infix to postfix

Các biểu thức đại số được sử dụng hằng ngày đều được biểu diễn dưới dạng trung tố (infix). Cách biểu diễn này rất dễ hiểu với con người vì hầu hết các toán tử (+, -, *, /) đều là toán tử hai ngôi và chúng phân cách giữa hai toán hạng với nhau. Tuy nhiên đối với máy tính, để tính được giá trị của một biểu thức đại số theo dạng này không đơn giản như ta vẫn làm. Để khắc phục điều đó, máy tính cần chuyển cách biểu diễn các biểu thức đại số từ trung tố sang một dạng khác là tiền tố hoặc hậu tố.

Thế nào là biểu thức tiền tố, trung tố và hậu tố

Trong đoạn giới thiệu trên có lẽ bạn cũng hình dung được thế nào là biểu thức trung tố, hiểu đơn giản tức là toán tử sẽ được đặt giữa hai toán hạng, dĩ nhiên đây phải là toán tử hai ngôi. Vậy dựa vào vị trí của của toán tử, liệu ta có thể biểu diễn biểu thức đại số dưới dạng khác? Câu trả lời là được, và như đã nói, ta có ba cách là biểu thức tiền tố (prefix), trung tố (infix) và hậu tố (postfix). Hãy xem một chút giới thiệu về cách biểu diễn biểu thức tiền tố và hậu tố để hiểu rõ hơn về chúng.

– Prefix: Biểu thức tiền tố được biểu diễn bằng cách đặt toán tử lên trước các toán hạng. Cách biểu diễn này còn được biết đến với tên gọi “ký pháp Ba Lan” do nhà toán học Ba Lan Jan Łukasiewicz phát minh năm 1920. Với cách biểu diễn này, thay vì viết x+y như dạng trung tố, ta sẽ viết +xy. Tùy theo độ ưu tiên của toán tử mà chúng sẽ được sắp xếp khác nhau, bạn có thể xem một số ví dụ ở phía sau phần giới thiệu này.

– Postfix: Ngược lại với cách Prefix, tức là các toán tử sẽ được đặt sau các toán hạng. Cách biểu diễn này được gọi là “ký pháp nghịch đảo Ba Lan” hoặc được viết tắt là RPN (Reverse Polish notation), được phát minh vào khoảng giữa thập kỷ 1950 bởi một triết học gia và nhà khoa học máy tính Charles Hamblin người Úc.

Một số ví dụ:

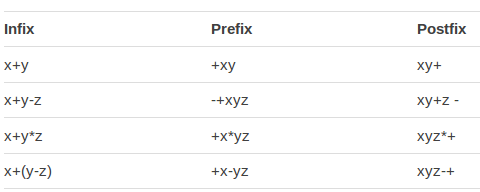
Phương pháp chuyển từ biểu thức trung tố sang hậu tố

Độ ưu tiên của các toán tử

Một trong những điều quan trọng trước khi bắt đầu là phải tính toán được độ ưu tiên của các toán tử trong biểu thức nhập vào. Để đơn giản ta chỉ xét các toán tử hai ngôi và thường dùng bao gồm: multiply (+),subtract (-), multiply (*), divide (/). Theo đó các toán tử “*, /” có cùng độ ưu tiên và cao hơn hai toán tử “+, -”. Như vậy ta có phương thức lấy độ ưu tiên toán tử như sau:

public int priority(char c){		// thiet lap thu tu uu tien
		if (c == '+' || c == '-') return 1;
		else if (c == '*' || c == '/') return 2;
		else return 0;
	}

Kiểm tra toán tử và toán hạng

Trong thuật toán chuyển đổi này ta cần có các phương thức kiểm tra xem một thành phần của chuỗi có phải là toán tử hoặc toán hạng không. Thay vì sử dụng các cấu trúc if hoặc switch dài dòng và bất tiện khi phát triển, ta sẽ dùng Regex để kiểm tra.
Ngoài ra vì chuỗi nhập vào là một biểu thức đại số, nên các toán hạng ta sẽ xét không chỉ là các chữ số mà còn có chữ cái từ a-z và A-Z.
Có một quy tắc nữa là khi dùng chữ cái thì chỉ cho phép duy nhất một chữ cái đại diện cho một toán hạng, còn khi dùng chữ số thì có thể nhiều chữ số ghép thành một toán hạng.

public boolean isOperator(char c){ 	// kiem tra xem co phai toan tu
		char operator[] = { '+', '-', '*', '/', ')', '(' };
		Arrays.sort(operator);
		if (Arrays.binarySearch(operator, c) > -1)
			return true;
		else return false;
	}

Chuẩn hóa biểu thức Infix trước khi chuyển đổi

Các biểu thức Infix khi nhập vào có thể dư thừa các khoảng trắng, các kí tự không phù hợp hoặc viết sai cú pháp.
Phần này các bạn xem bài chuẩn hóa xâu trong Java

Ngoài ra các bạn còn phải ghép các chữ số liền nhau thành số (toán hạng), tách các toán tử, phân cách với nhau bằng một khoảng trắng. Các phần tử này tôi sẽ gọi là một token.

public String[] processString(String sMath){ // xu ly bieu thuc nhap vao thanh cac phan tu
		String s1 = "", elementMath[] = null;
		InfixToPostfix  IFP = new InfixToPostfix();
		sMath = sMath.trim();
		sMath = sMath.replaceAll("\s+"," "); //	chuan hoa sMath
		for (int i=0; i<sMath.length(); i++){
			char c = sMath.charAt(i);//sMath.substring(i,1);
			if (!IFP.isOperator(c))
				s1 = s1 + c;
			else s1 = s1 + " " + c + " ";
		}
		s1 = s1.trim();
		s1 = s1.replaceAll("\s+"," "); //	chuan hoa s1
		elementMath = s1.split(" "); //tach s1 thanh cac phan tu
		//System.out.println(s1);
		return elementMath;
	}

Thuật toán để chuyển một biểu thức Infix sang dạn Prefix:

Đọc từng token trong biểu thức infix từ trái qua phải, với mỗi token ta thực hiện các bước sau:
– Nếu là toán hạng: cho ra output.
– Nếu là dấu mở ngoặc “(“: cho vào stack
– Nếu là dấu đóng ngoặc “)”: lấy các toán tử trong stack ra và cho vào output cho đến khi gặp dấu mở ngoặc “(“. (Dấu mở ngoặc cũng phải được đưa ra khỏi stack)
– Nếu là toán tử:
+/Chừng nào ở đỉnh stack là toán tử và toán tử đó có độ ưu tiên lớn hơn hoặc bằng toán tử hiện tại thì lấy toán tử đó ra khỏi stack và cho ra output.
+/Đưa toán tử hiện tại vào stack
Sau khi duyệt hết biểu thức infix, nếu trong stack còn phần tử thì lấy các token trong đó ra và cho lần lượt vào output.

VD: Chúng ta sẽ chuyển biểu thức A*B+C*((D-E)+F)/G từ dạng Infix sang dạng Postfix: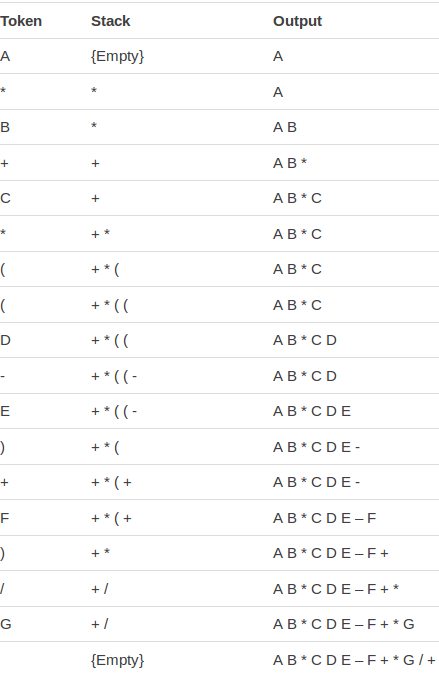

Cài đặt trên Java

public String[] postfix(String[] elementMath){
		InfixToPostfix  IFP = new InfixToPostfix();
		String s1 = "", E[];
		Stack <String> S = new Stack <String>();
		for (int i=0; i<elementMath.length; i++){ 	// duyet cac phan tu
			char c = elementMath[i].charAt(0);	// c la ky tu dau tien cua moi phan tu

			if (!IFP.isOperator(c)) 		// neu c khong la toan tu
				s1 = s1 + " " + elementMath[i];		// xuat elem vao s1
			else{						// c la toan tu
				if (c == '(') S.push(elementMath[i]);	// c la "(" -> day phan tu vao Stack
				else{
					if (c == ')'){			// c la ")"
						char c1;		//duyet lai cac phan tu trong Stack
						do{
							c1 = S.peek().charAt(0);	// c1 la ky tu dau tien cua phan tu
							if (c1 != '(') s1 = s1 + " " + S.peek(); 	// trong khi c1 != "("
							S.pop();
						}while (c1 != '(');
					}
					else{
						while (!S.isEmpty() && IFP.priority(S.peek().charAt(0)) >= IFP.priority(c)){
						// Stack khong rong va trong khi phan tu trong Stack co do uu tien >= phan tu hien tai
							s1 = s1 + " " + S.peek();	// xuat phan tu trong Stack ra s1
							S.pop();
						}
						S.push(elementMath[i]); // 	dua phan tu hien tai vao Stack
					}
				}
			}
		}
		while (!S.isEmpty()){	// Neu Stack con phan tu thi day het vao s1
			s1 = s1 + " " + S.peek();
			S.pop();
		}
		E = s1.split(" ");	//	tach s1 thanh cac phan tu
		return E;
	}

Và cuối cùng là chạy chuơng trình chính:

public static void main(String[] agrs){
		String sMath, elementMath[] = null;
		InfixToPostfix  IFP = new InfixToPostfix();
		Scanner input = new Scanner(System.in);
		sMath = input.nextLine();					// 	nhap bieu thuc
		elementMath = IFP.processString(sMath);		//	tach bieu thuc thanh cac phan tu
		elementMath = IFP.postfix(elementMath);		// 	dua cac phan tu ve dang postfix
		for (int i=0; i<elementMath.length; i++)	// 	xuat dang postfix
			System.out.print(elementMath[i] + " ");
		input.close();
	}

Để kiểm tra kết quả có chính xác không, bạn có thể dùng một dịch vụ chuyển đổi trực tuyến tại đây . Trang web cũng sẽ thực hiện tính toán giá trị của biểu thức sau khi chuyển đổi.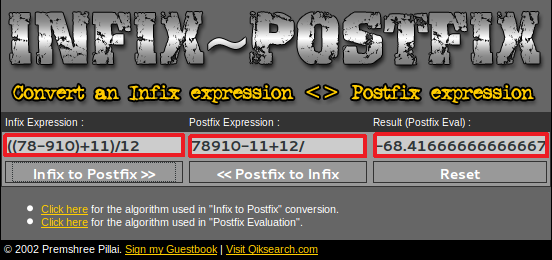

Từ đây ta có thể xây dựng được cách Tính giá trị của biểu thức hậu tố