Time-Series Data
Time-series Data : là một chuỗi các điểm dữ liệu, thường bao gồm các phép đo liên tiếp được thực hiện từ cùng một nguồn trong một khoảng thời gian. Phân tích chuỗi thời gian có mục đích nhận đang và tập hợp lại các yếu tố, những biến đổi theo thời gian mà nó có ảnh hưởng đến giá trị của biến quan ...
Time-series Data: là một chuỗi các điểm dữ liệu, thường bao gồm các phép đo liên tiếp được thực hiện từ cùng một nguồn trong một khoảng thời gian. Phân tích chuỗi thời gian có mục đích nhận đang và tập hợp lại các yếu tố, những biến đổi theo thời gian mà nó có ảnh hưởng đến giá trị của biến quan sát.
Trong Time-series Data, có hai loại chính.
- Chuỗi thời gian thông thường (regular time series), loại thông thường được gọi là số liệu.
- Chuỗi thời gian bất thường (events) là những sự kiện.
Ứng dụng: Time-series data được ứng dụng rất rộng rãi trong các lĩnh vực:
- IoT
- DevOps
- Phân tích thời gian thực
- Dự báo kinh tế
- Tính toán doanh số bán hàng
- Phân tích lãi
- Phân tích thị trường
- Kiểm soát quy trình và chất lượng
- Phân tích điều tra
- …….
Tùy thuộc vào ý định và ứng dụng của người dùng mà sẽ có những phương pháp xử lý dữ liệu thời gian thực khác nhau. Trong bài này sẽ xem xét 2 kĩ thuật phân tích sau:
- Phương pháp trung bình
- Kĩ thuật liên tiến lũy thừa
Phương pháp trung bình
Chúng ta sẽ cùng xem xét 1 số phương pháp trung bình, chẳng hạn như phương pháp trung bình đơn giản với các dữ liệu trong quá khứ.
1 quản lý nhà băng muốn biết khách hàng điển hình sẽ gửi tiết kiệm bao nhiêu tiền(đơn vị 1000$$. Anh ta chọn 12 khách hàng bất kì và cho kết quả sau:
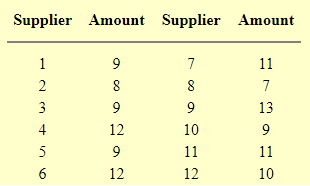
Giá trị trung bình mà máy tính tính ra là 10. Người quản lý quyết định sử dụng số liệu này làm dự toán chi tiêu của một nhà cung cấp thông thường.
Nhưng đây là cách tính toán tốt hay cách tính toán tồi?
Chúng ta sử dụng phương pháp “Bình phương bình quân lỗi”:
-
"error" = số tiền thực đã trừ trừ số tiền ước tính.
-
"error squared" là lỗi ở trên, bình phương.
-
Các "SSE" là tổng của các bình phương lỗi.
-
Các "MSE" là trung bình của các bình phương lỗi.
Ta có kết quả:
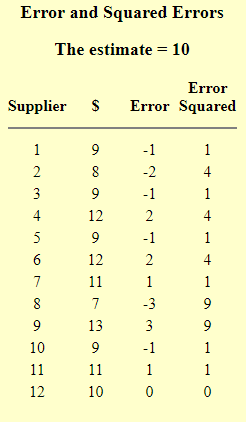
SSE=36 và MSE=36/12=3
Vậy ước tính của số tiền chi cho mỗi nhà cung cấp là bao nhiêu? Hãy so sánh ước tính (10) với các ước tính sau: 7, 9 và 12. Tức là, chúng ta ước tính rằng mỗi nhà cung cấp sẽ chi tiêu 7, hoặc 9 hoặc $$12.
Tiếp tục tính toán chúng ta sẽ có bảng sau:

Ước tính tốt nhất ở đây là ước tính với MSE thấp nhất.
Bảng tiếp theo đây sẽ là thống kê doanh thu chưa qua thuế của các cty máy tính từ 1985-1994:
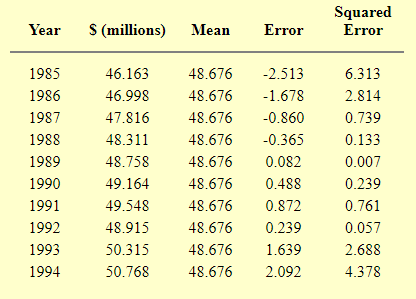
MSE = 1.8129
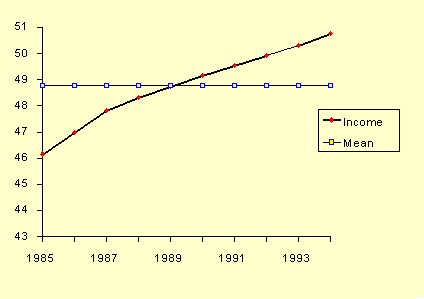
Chúng ta có thể dựa vào số liệu trên để có 1 biểu đồ dự đoán xu hướng
Phương pháp liên tuyến lũy thừa
Đây là phương pháp dự đoán dựa trên dữ liệu gần nhất cộng với phần trăm chênh lệch giữa số dự đoán và số thực tế ở thời điểm dự đoán. Là phương pháp được sử dụng nhiều nhất trong tất cả các phương pháp dự đoán. Nó là phần không thể thiếu được trong các chương trình dự đoán bằng lập trình vi tính và được sử dụng rộng rãi trong quản lý đặt hàng ở các công ty bán lẻ, bán sỉ và các công ty dịch vụ. Nó phân làm 3 loại:
Phương pháp liên tiến lũy thừa đơn (Simple Exponential Smoothing):
Phương pháp này áp dụng cho dãy dữ liệu ổn định, không thay đổi nhiều, không có xu hướng, không theo mùa.

Hằng số liên tiến (alpha) thể hiện độ đáp ứng đối với sự chênh lệch giữa dự đoán và thực tế. Hằng số này được quyết định bởi bản thân của sản phẩm cũng như cảm nhận của nhà quản lý. Chẳng hạn, một nhà sản xuất một sản phẩm mà nhu cầu tương đối ổn định thì tỷ lệ đáp ứng với sự chênh lệch giữa dự đoán và thực tế sẽ nhỏ. Nếu nhu cầu tăng trưởng nhanh, tỷ lệ này sẽ tăng cao. Hằng số này có giá trị từ 0 đến 1. Ðể tìm số alpha chính xác nhất thì phảI dùng phương pháp thử sai, alpha sẽ là giá trị mà làm cho độ lệch trị tuyệt đốI trung bình (Mean Absolute Deviation-MAD) là nhỏ nhất.
MAD được tính bằng trung bình cộng của độ lệch giữa dự đoán và thực tế, sau khi đã lấy trị tuyệt đối.
Công thức tính MAD:

Ví dụ ta có số liệu về như cầu mở tài khoản tiền mặt trong 3 tháng đầu năm, giả sử dự đoán đã tính trong tháng 1 là 706. Ta sẽ tính được dự đoán cho tháng 4.
| Tháng | Thực tế | Dự đoán |
|---|---|---|
| 1 | 721 | 706 |
| 2 | 816 | 709 |
| 3 | 671 | 730 |
| 4 | 718 |
Vậy làm sao để tính được dự đoán cho các tháng tiếp theo (5, 6, 7...) khi không có dữ liệu thực tế? Ta sẽ dùng kỹ thuật bootstrapping theo công thức:
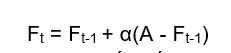
Trong đó A là dữ liệu thực thế cuối cùng ta có. Vậy ta sẽ dự đoán được số liệu tiếp theo theo kỹ thuật này.
| Tháng | Thực tế | Dự đoán |
|---|---|---|
| 1 | 721 | 706 |
| 2 | 816 | 709 |
| 3 | 671 | 730 |
| 4 | 718 | |
| 5 | 709 | |
| 6 | 701 |
Phương pháp liên tiến lũy thừa kép (Double Exponential Smoothing, Trend-adjusted Exponential Smoothing, Holt’s Exponential Smoothing)
Phương pháp này áp dụng cho dãy dữ liệu có xu hướng, không có tính chất mùa.

Khi tồn tại một xu hướng, có thể xu hướng tăng hoặc giảm, thì kết quả dự đoán bằng phương pháp liên tiến lũy thừa đơn luôn luôn lệch xa so với thực tế, có thể thấp hơn hoặc cao hơn. Phương pháp liên tiến lũy thừa kép đã giảI quyết được vấn đề này bằng cách sử dụng hai hằng số. Hằng số alpha thì đã trình bày ở trên. Hằng số beta sẽ làm giảm ảnh hưởng của sai số xảy ra giữa thực tế và dự đoán do tồn tại xu hướng lên xuống.
Hai hằng số này nằm trong giá trị từ 0 đến 1. Tương tự, để tính chính xác nhất alpha và beta thì dùng phương pháp thử sai. Số alpha và beta sẽ là trị giá để cho độ lệch trị tuyệt đối trung bình (MAD) và độ lệch phần trăm trị tuyệt đối trung bình (Mean Absolute Percentage Error-MAPE) nhỏ nhất.
Cách tính MAPE như sau:

Số liệu dưới đây là doanh số bán hàng trong 10 tháng của một công ty. Dùng phương pháp liên tiến lũy thừa kép để dự đoán doanh số bán hàng trong tháng thứ 11.

Ta dùng 4 tháng đầu để tính dự đoán cho tháng thứ 4 (tháng lấy làm mốc).
Độ lệch trung bình từ tháng 1-4: (728-700)/3 = 9.33
Dự đoán bán hàng trong tháng 4: 728+9.33 = 737.3
Lấy alpha=0.4, beta=0.3, ta có bảng sau:
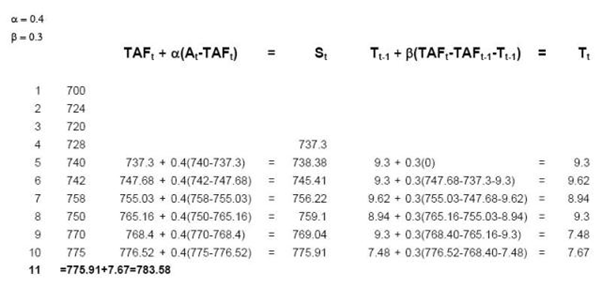
Như vậy dự đoán trong tháng thứ 11 sẽ là 783.58.
Phương pháp liên tiến lũy thừa theo mùa (Seasonal adjusted Exponential Smoothing, Winter’s Exponential Smoothing)
Một số sản phẩm tiêu thụ theo mùa, ví dụ như sản phẩm áo tắm thì tiêu thụ mạnh vào mùa hè. Vì vậy khi dự đoán phải tính chỉ số mùa (seasonal index) thì kết quả mới chính xác.
Số liệu dưới đây được ghi nhận trong 2 tuần trước và theo chu kỳ trong tuần vào ngày thứ 4, nhu cầu tăng vọt. Dùng phương pháp liên tiến lũy thừa theo mùa (seasonal adjusted exponential smoothing) để dự đoán nhu cầu vào thứ hai tuần này với alpha=0.3 và beta=0.2.
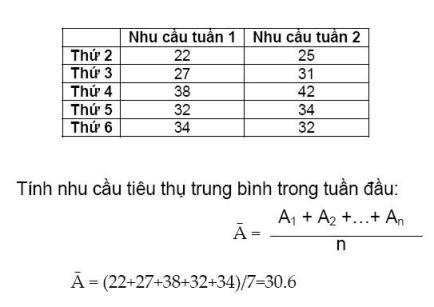
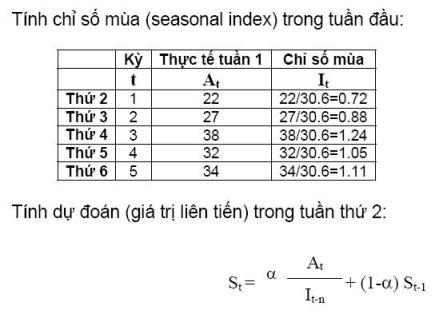
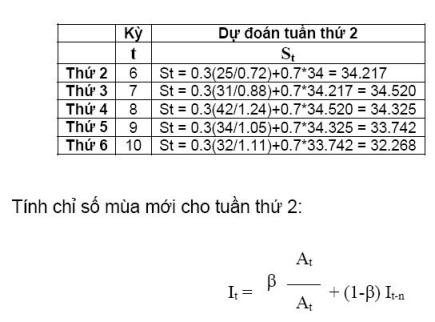
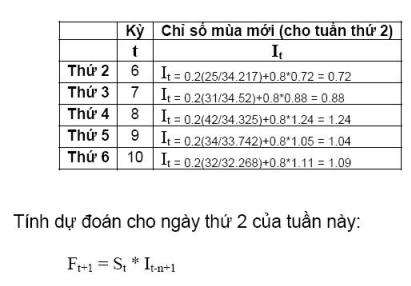
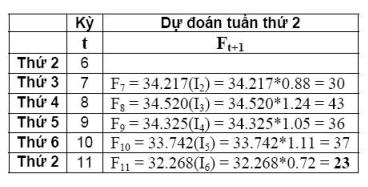
Như vậy, ngày thứ 2 tuần này nhu cầu sẽ là 23 (Đây là dự đoán ứng với alpha=0.3 và beta=0.2, muốn dự báo chính xác thì dùng phương pháp thử sai để tìm alpha và beta, sau đó tính giá trị dự đoán tương ứng.
Time-series database được tối ưu hóa để thu thập, lưu trữ, truy xuất và xử lý dữ liệu time-series. Ở đây chúng ta khảo sát ví dụ với InfluxDB
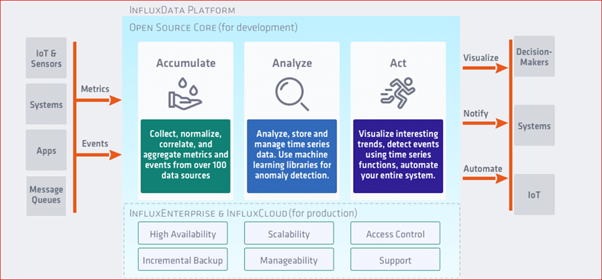
InfluxDB được thiết kế để làm việc với dữ liệu chuỗi thời gian. Cơ sở dữ liệu SQL có thể xử lý chuỗi thời gian nhưng không được tạo ra cho mục đích đó. Nói tóm lại, InfluxDB được thực hiện để lưu trữ một khối lượng dữ liệu chuỗi thời gian lớn và thực hiện phân tích theo thời gian về những dữ liệu đó một cách nhanh chóng.
Thời gian là tất cả.
Trong InfluxDB, dấu thời gian xác định một điểm duy nhất trong bất kỳ chuỗi dữ liệu nhất định. Điều này giống như một bảng cơ sở dữ liệu SQL, nơi khoá chính được thiết lập trước bởi hệ thống và luôn luôn là thời gian. InfluxDB cũng nhận ra rằng sở thích graph của bạn có thể thay đổi theo thời gian. Trong InfluxDB bạn không phải định nghĩa các lược đồ lên phía trước. Các điểm dữ liệu có thể có một trong các trường trên một phép đo, tất cả các trường trên phép đo hoặc bất kỳ số nào ở giữa. Bạn có thể thêm các trường mới vào một phép đo bằng cách viết một điểm cho trường mới đó.
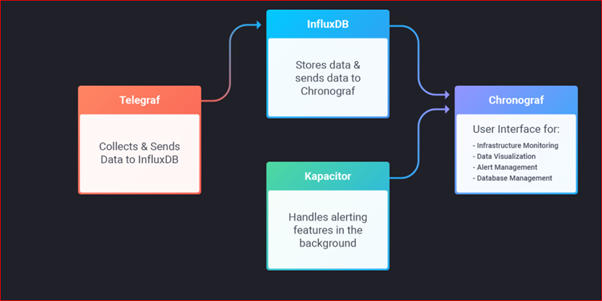
Telegraf là một đại lý viết trong Go để thu thập số liệu và viết chúng vào InfluxDB hoặc các đầu ra có thể khác.
Chronograf là thành phần giao diện người dùng của InfluxData.
Các bạn có thể tìm hiểu thêm về InfluxDB ở đây: https://www.influxdata.com/ . Chúng mình đã thử demo với thống kê lượng năng lượng, dữ liệu, bộ nhớ bị tiêu hao trên máy tính bởi các ứng dụng khá là hay(tiếc là bị mất demo, nhưng làm cũng đơn giản thôi ấy mà)
Dữ liệu thời gian thực rất quan trọng đối với cuộc sống hiện đại và là 1 phần quan trọng của big data hiện nay khi 1 doanh nghiệp làm dữ liệu thời gian thực có thể nhận tới hàng gigabyte mỗi giờ. Vì vậy, cần có cách thu thập và xử lý hợp lý với loại dữ liệu này.
Đây là bài báo cáo nhóm môn Data Modeling mình làm chung với bạn Nguyễn Gia Cường, Việt Nhật AS k59. Mình phụ trách phần nửa đầu lý thuyết và Cường làm việc với InfluxDB ở phần nửa sau.
