Big-O giải thích bởi 1 lập trình viên tự học
Bài viết được dịch từ Big-O notation explained by a self-taught programmer của tác giả Justin Abrahms. Kí hiệu Big-O đã từng là 1 thuật ngữ đáng sợ đối với tôi. Tôi đã nghĩ đó là cách mà những lập trình viên "đích thực" nói về code của họ. Nó càng đáng sợ hơn bởi vì những chú giải mang tính chất ...
Bài viết được dịch từ Big-O notation explained by a self-taught programmer của tác giả Justin Abrahms.
Kí hiệu Big-O đã từng là 1 thuật ngữ đáng sợ đối với tôi. Tôi đã nghĩ đó là cách mà những lập trình viên "đích thực" nói về code của họ. Nó càng đáng sợ hơn bởi vì những chú giải mang tính chất học thuật (ví dụ như Wikipedia) không làm cho nó dễ hiểu hơn chút nào. Điều tôi muốn nói đến ở bài này là những khái niệm cơ bản của Big-O không đến nỗi khó như vậy.
Nói cho đơn giản thì Big-O là cách mà những lập trình viên nói về thuật toán. Thuật toán lại là 1 chủ đề đáng sợ khác mà tôi sẽ thảo luận ở 1 bài viết trong tương lai, nhưng đối với bài viết này thì hãy coi 1 thuật toán nghĩa là 1 hàm trong chương trình của bạn (thật ra nó cũng gần đúng như vậy). Big-O của 1 hàm được xác định thông qua cách nó phản hồi đối với những độ lớn đầu vào khác nhau. Nó sẽ chậm đi như thế nào nếu chúng ta bắt nó xử lý 1 danh sách gồm 1000 thứ thay vì 1 danh sách chỉ có 1 thứ?
Hãy xem đoạn code sau:
def item_in_list(to_check, the_list):
for item in the_list:
if to_check == item:
return True
return False
Nếu chúng ta gọi item_in_list(2, [1,2,3]), hàm này sẽ chạy khá nhanh. Chúng ta có 1 vòng lặp để kiểm tra xem list có chứa argument đầu tiên trong hàm không, nếu có thì trả về True. Nếu chúng ta chạy đến cuối list mà vẫn không tìm thấy thì trả về False.
"Độ phức tạp" của hàm này là O(n). Tôi sẽ giải thích ý nghĩa của nó ngay, nhưng hãy cùng phân tích cái cú pháp toán học này trước đã nhé. O(n) có nghĩa là "Bậc của N" bởi vì hàm O còn được biết đến là hàm bậc (Order). Tôi nghĩ đó là bởi vì chúng ta đang ước lượng, mà ước lượng thì lại liên quan đến "orders of magnitude".
"Orders of magnitude" lại là 1 thuật ngữ toán học khác mà về cơ bản thì nó chỉ ra sự khác biệt giữa các cấp độ của con số. Hãy nghĩ về sự khác biệt giữa số 10 và số 100. Nếu bạn nghĩ đến 10 người bạn thân nhất so với nghĩ đến 100 người, đó là 1 sự khác biệt rất lớn. Tương tự, khác biệt của 1,000 và 10,000 cũng rất lớn (thật ra thì nó là sự khác biệt giữa 1 cái xe phế thải và 1 cái xe mới dùng vài lần). Hóa ra là trong việc ước lượng, miễn là bạn vẫn nằm trong 1 order of magnitude thì đã là gần đúng rồi. Nếu bạn phải đoán số kẹo nằm trong 1 cái máy, bạn sẽ nằm trong 1 order of magnitude nếu bạn nói là 200. 10,000 cái kẹo thì sẽ RẤT sai.

Hình 1: 1 máy gumball chứa số gumball nằm trong order of magnitude của 200
Trở lại với việc phân tích O(n), nó có nghĩa rằng nếu chúng ta phải ước lượng thời gian mà nó cần để chạy hàm này với những độ lớn đầu vào khác nhau (ví dụ như 1 array gồm 1 item, 2 item, 3 item,...), chúng ta sẽ thấy rằng thời gian ước tính có liên quan đến số item nằm trong array. Cái này gọi là đồ thị tuyến tính. Nghĩa là đường kẻ về cơ bản sẽ là đường thẳng nếu chúng ta vẽ nó ra.
Có thể bạn sẽ phát hiện ra rằng nếu, với đoạn code mẫu ở trên, item cần tìm luôn luôn là item đầu tiên trong list, đoạn code của chúng ta sẽ chạy rất nhanh! Điều này không sai, nhưng Big-O hoàn toàn là để ước tính hiệu suất để làm 1 công việc nào đó trong tình huống xấu nhất. Tình huống xấu nhất đối với đoạn code trên là thứ chúng ta đang tìm không hề nằm trong list. (Thuật ngữ toán học cho cái này là "cận trên")
Nếu bạn muốn xem 1 đồ thị biểu diễn những hàm này, bạn sẽ bỏ qua hàm O() và thay biến n bằng x. Sau đó thì bạn có thể gõ nó vào Wolfram Alpha bằng "plot x" và nó sẽ show ra 1 đường chéo. Lí do bạn cần thay n bằng x là do chương trình biểu diễn đồ thị của họ muốn x là tên biến bởi vì nó liên quan đến cột x. Cột x sẽ to ra từ trái qua phải tương ứng với độ lớn tăng dần của array truyền vào hàm của bạn. Cột y thể hiện thời gian, nên nếu đường thẳng đi lên càng cao thì nó càng chậm.
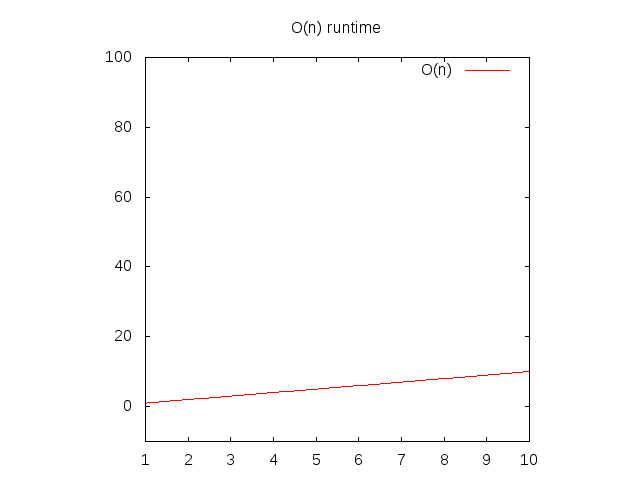
Hình 2: Đặc điểm runtime của 1 hàm O(n)
Vậy thì những ví dụ khác của nó sẽ thế nào?
Hãy xem hàm sau:
def is_none(item):
return item is None
Đây là 1 ví dụ ngớ ngẩn, nhưng tạm thời hãy chịu vậy nhé. Hàm này được gọi là O(1) hay "độ phức tạp hằng số". Nó có nghĩa là không cần biết đầu vào lớn đến đâu, nó luôn chỉ cần 1 thời gian cố định để xử lý. Nếu bạn quay lại Wolfram và gõ "plot 1", bạn sẽ thấy rằng nó luôn cố định, bất kể là bạn đi sang phải xa đến đâu. Nếu bạn cấp cho nó 1 list gồm 1 triệu số nguyên, nó cũng sẽ chỉ cần số thời gian tương tự như là bạn truyền vào 1 list có 1 số nguyên. Thời gian cố định được coi là tình huống tốt nhất của 1 hàm.
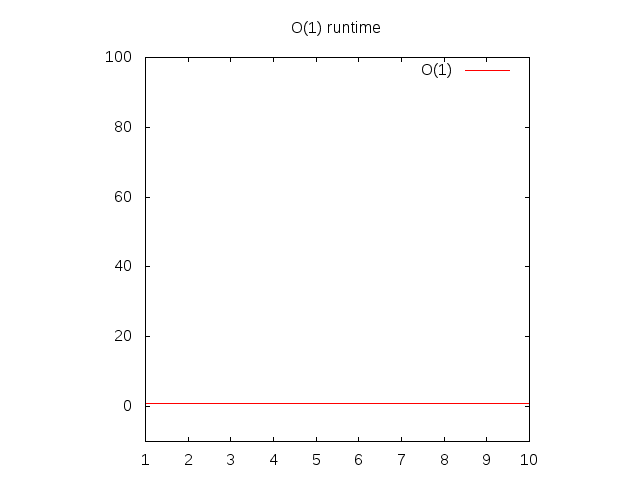
Hình 3: Đặc điểm runtime của 1 hàm O(1)
Hãy xem hàm sau:
def all_combinations(the_list):
results = []
for item in the_list:
for inner_item in the_list:
results.append((item, inner_item))
return results
Hàm này ghép mỗi item trong list với những item khác trong list. Nếu chúng ta truyền vào 1 array [1,2,3], nó sẽ trả về [(1,1) (1,2), (1,3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]. Cái này là 1 phần của toán tổ hợp (lại 1 thuật ngữ đáng sợ khác). Hàm này (hay thuật toán này, nếu bạn muốn tỏ ra nguy hiểm (hihi)) được coi là O(n^2). Đó là bởi vì với mỗi item trong list (hay n thể hiện độ lớn đầu vào), chúng ta cần phải làm thêm n lần tính toán. Mà n * n = n^2.
Dưới đây là đồ thị so sánh các độ phức tạp trên, để tham khảo. Bạn có thể thấy rằng hàm O(n^2) sẽ chậm đi rất nhanh trong khi những hàm cần thời gian cố định để xử lý lại tốt hơn rất nhiều. Điều này đặc biệt tốt đối với xử lý cấu trúc dữ liệu, chủ đề mà tôi cũng sẽ nói đến sớm thôi.
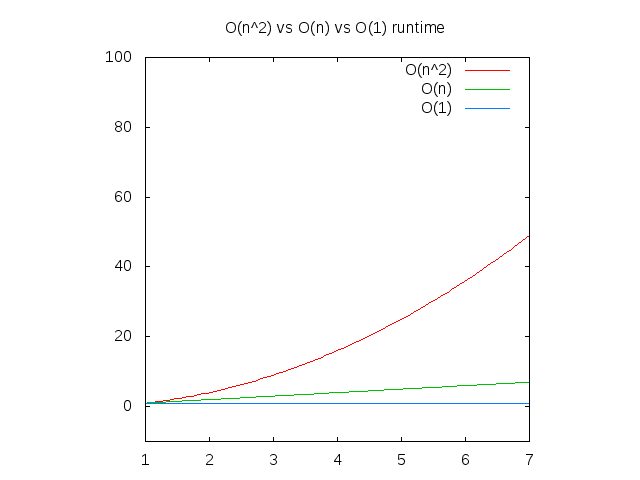
Figure 4: So sánh O(n2) vs O(n) vs O(1)
Trên đây là những hiểu biết có cấp độ tương đối cao về Big-O, nhưng tôi mong rằng bạn sẽ nhanh chóng quen thuộc với thuật ngữ này. Có 1 khóa học coursera có thể cho bạn những khía cạnh sâu hơn vào chủ đề này, nhưng xin báo trước là nó sẽ liên quan rất nhiều đến toán học. Nếu có bất cứ thứ gì trong bài này mà bạn không hiểu, hãy gửi email cho tôi nhé.
