Giải đề Pre ACM PTIT 2015 round 1

SPOJ PTIT PRE ACM 2015

Problem A: Các cặp giai thừa

P151PROA spoj , CF #292 (Div. 2) C. Drazil and Factorial

Thuật toán: Tham lam

F(x) = tích của các F(các chữ số của a). Với mỗi chữ số c của a, ta thực hiện quy đổi nó sang một nhóm X, sao cho F(c) = F(X) và X có nhiều chữ số nhất.

Ta có:

c –> X

0, 1 -> empty

2 -> 2

3 -> 3

4 -> 322

5 -> 5

6 -> 53

7 -> 7

8 -> 7222

9 -> 7332

Sau đó sắp xếp các chữ số theo thứ tự giảm dần, rồi in ra đáp số. Đọc input bằng xâu sẽ dễ

dàng trong việc xử lý hơn.

code mẫu: https://kienthuc24h.com/p151proa-spoj-cf-292-div-2-c-drazil-and-factorial/

Problem B: Rubik đi siêu thị

Thuật toán: quy hoạch động.

Gọi F là kết quả với F[i] là giá trị nhỏ nhất khi mua được i món hàng.

Khi nhập món hàng thứ i thì ta có 2 khả năng:

– Chọn món hàng thứ i nhân viên thu ngân kiểm tra, sẽ mất t_i giây và lúc đó sẽ ăn trộm thêm được t_i món hàng, cộng với cả món hàng thứ i thì sẽ có i + t_i + 1 món hàng được lấy bao gồm cả của Rubik và số món hàng để lại thanh toán và ta sẽ có mối liên hệ giữa f[j + t_i + 1] với f[j] với j bất kì.

– Món hàng thứ i có thể được ăn trộm từ thời gian của các món hàng trước, trường hợp này đã được xét ở trên với j bất kì.

Kết quả bài toán sẽ là f[n] khi cả n món đều đã được lấy hết.

Problem C: Trò chơi trí tuệ

Thuật toán: lý thuyết trò chơi, quy hoạch động trạng thái.

Với tập số nguyên A = {1, 2, …, n}, ký hiệu POW(x) = {x, x^2, x^3, … , x^s} với x^s là lũy thừa lớn nhất không vượt quá n. Ta có s_max = 29 vì 2^30 > 10^9.

Bài toán yêu cầu, với mỗi bước, chọn một tập POW(x) và loại nó khỏi tập hợp A ban đầu, đến khi tập A không còn phần tử nào nữa.

Ta gọi tập hợp POW(x) với x thỏa mãn điều kiện x không là lũy thừa (bậc >= 2) của bất kì số nguyên nào là tập hợp tối giản. Ví dụ POW(2), POW(3), POW(5), POW(7), POW(10), …

Dễ thấy với số nguyên k bất kì, nó chỉ thuộc một tập hợp POW(x) tối giản duy nhất.

Bài toán được chia nhỏ thành các trò chơi con độc lập, mỗi phép chơi thực hiện trên các tập hợp POW(x) tối giản, kết quả cuối cùng bằng tổng Nim của các hàm Grundy của tất cả các trò chơi con độc lập. Ta chỉ cần quan tâm với mỗi s (giá trị từ 1 -> 29), số lượng các tập hợp tối giản có bậc bằng s bằng bao nhiêu. Rõ ràng nếu k >= sqrt(n) và k không nằm trong các tập hợp POW(x) tối giản nào với x từ 1 -> sqrt(n), thì k thuộc nhóm tập hợp tối giản có bậc s = 1.

Xét bài toán con độc lập trong tập hợp POW(x) = {x, x^2, x^3, … , x^s}, mỗi bước chọn một số và loại bỏ đi các lũy thừa của nó ra khỏi tập hợp. Bài toán tương đương với cho tập X = {1, 2, 3, …, s}, mỗi bước chơi chọn lấy một số và loại bỏ các bội của nó ra khỏi tập hợp.

Chúng ta cần tìm hàm Sprague – grundy cho trò chơi này.

Hàm Sprague – grundy (SG) của một đồ thị G = (X, F) được định nghĩa như sau:

Mỗi đỉnh x của đồ thị được gắn một số g(x) là số nguyên không âm nhỏ nhất không nằm trong tập các giá trị g(y) của các đỉnh y tới được từ x. Nếu đỉnh x là đỉnh kết thúc thì g(x) = 0.

Hay g(x) = min{n>=0, với mọi y thuộc F(x), n khác G(y)}

Ta sử dụng quy hoạch động trạng thái để tìm hàm Grundy cho trò chơi trên tập X với mỗi tập hợp gồm các giá trị từ 1 -> s.

Ví dụ xét X = {1, 2, 3}

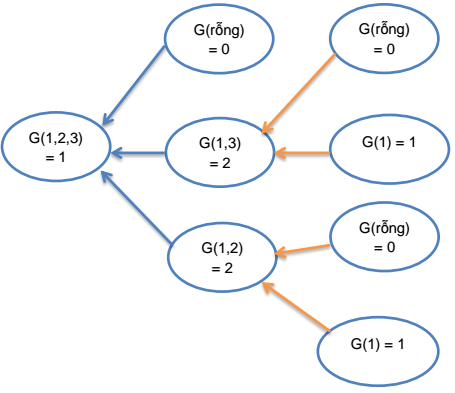
Đoạn code tìm hàm Sprague – grundy:

Problem D: Du hành giữa các vì sao

Thuật toán: quy hoạch động trên cây

Với mỗi trạm thứ i ta giả sử đấy là trạm đích cần chuyển đến, dân ở các trạm khác sẽ di chuyển đến trạm i qua n – 1 không gian tốn n – 1 giá trị tài nguyên, sắp xếp các giá trị ấy ta sẽ được kết quả.

Trạm thứ i để tính được n – 1 giá trị trên, để dễ dàng tính toán ta coi trạm i là gốc, người dân sẽ di chuyển từ các trạm là nút lá lên các nút cha của nó và nút u di chuyển đến nút cha của nó khi không còn người dân nào ở nút con của nó, gọi dp[u] là số dân ở trạm u sau khi người dân ở nút con v của nó di chuyển hết lên u thì dp[u] = d[u] + dp[v] và giá trị tài nguyên ở không gian ấy là dp[v] * w[u][v].

Problem E: E Sản xuất kem

Thuật toán: Tham lam

Ta tính số khay được phun kem rồi lấy tổng số khay trừ đi.

Chia 3 trường hợp 2 máy phun cùng hàng, cùng cột và còn lại

Problem F: Cipher

[CF490C]HACKING CYPHER, P151PROF spoj Cipher

Thuật toán: Tham lam

Sử dụng 2 công thức sau: (a + b ) % c = (a % c + b % c) % c

Và (a * b) % c = ((a % c) * (b % c)) % c

Số ban đầu được chia thành 2 phần x và y, x chia hết cho a, y chia hết cho b.

Do đó, ta có được x % a = 0 và y % b = 0.

Gọi phần dư của số bắt đầu từ vị trí thứ nhất đến vị trí i khi chia cho a là modA[i], phần dư của số bắt đầu từ vị trí i đến vị trí cuối cùng khi chia cho b là modB[i].

Duyệt các vị trí i, vị trí i thỏa mãn yêu cầu đề bài là vị trí modA[i] = 0 và modB[i + 1] = 0, i < độ dài của số ban đầu.

code mẫu: https://kienthuc24h.com/cf490chacking-cypher-p151prof-spoj-cipher/

Problem G: Xếp hàng

P151PROG spoj PTIT – Xếp Hàng

Phân dãy sinh viên thành 2 dãy, một dãy là các sinh viên đứng ở vị trí chẵn, một dãy là các sinh viên đứng ở vị trí lẻ, sau đó gộp dãy.

Có thể xây dựng dãy các sinh viên ở vị trí lẻ bằng cách “nhảy” từ người có a = 0.

Dãy các sinh viên ở vị trí chẵn có thể xây dựng bằng phương pháp tương tự.

code mẫu: https://kienthuc24h.com/p151prog-spoj-ptit-xep-hang/

Problem H: Số ma thuật

Nhận thấy rằng các số 1, 14, 144 đều có số 1 ở đầu và trong mỗi số đó chỉ có 1 số 1 duy nhất.

Dov vậy cách làm của ta như sau tìm tất cả vị trí của các số một, giả sử vị trí 2 số 1 liên tiếp là i và j, giờ ta chỉ cần kiểm tra số từ vị trí i đến vị trí j – 1 có là một trong 3 số trên hay không.

Problem I: Các chữ số cuối cùng

P151PROI spoj PTIT

Một bài toán đơn giản, cách thực hiện y như đề bài.

code mẫu: https://kienthuc24h.com/p151proi-spoj-ptit-chu-so-cuoi-cung/

Problem J: Đếm số đường đi.

Thuật toán: Quy hoạch động, số học

Gọi ô (1, 1) là ST, ô (n, m) là END, ô bị chặn thứ i là P[i]. Coi ô (n, m) là ô bị chặn thứ k+1.

Gọi dp[i] = tổng số cách đi từ ô ST -> P[i] và không đi qua ô cấm nào (không tính P[i]).

Cách tính mảng dp:

dp[i] = số cách đi từ ô ST đến ô P[i] – số con đường đã đi qua ô cấm nào đó.

Cụ thể, gọi:

sumA[i] = số cách đi từ ô ST -> P[i]. Dễ thấy sumA[i] = C(P[i].x + P[i].y – 2, P[i].x – 1).

sumB[i] = số cách đi từ ô ST  P[i] và có đi qua ít nhất một ô cấm (không tính P[i]).

Ta có dp[i] = sumA[i] – sumB[i], và sumB[i] = tổng của tất cả các (dp[j] * số cách đi từ P[j] tới P[i]), với mọi j thỏa mãn điểm

P[j] nằm trong hình chữ nhật (1,1) -> (x[i], y[i]).

Phần còn lại là xử lí cách tính nhanh công thức tổ hợp C(n, k) theo modulo 1000000007, sử dụng mod nghịch đảo (định lý Fermat nhỏ).