Tìm hiểu thuật toán mã hóa khóa đối xứng AES

1. Tổng quan.

• AES (viết tắt của từ tiếng anh: Advanced Encryption Standard, hay Tiêu chuẩn mã hóa nâng cao) là một thuật toán mã hóa khối được chính phủ Hoa Kỳ áp dụng làm tiêu chuẩn mã hóa.
• Thuật toán được xây dựng dựa trên Rijndael Cipher phát triển bởi 2 nhà mật mã học người Bỉ: Joan Daemen và Vincent Rijmen.
• AES làm việc với các khối dữ liệu 128bit và độ dài khóa 128bit, 192bit hoặc 256bit. Các khóa mở rộng sử dụng trong chu trình được tạo ra bởi thủ tục sinh khóa Rijndael.
• Hầu hết các phép toán trong thuật toán AES đều thực hiện trong một trường hữu hạn của các byte. Mỗi khối dữ liệu đầu vào 128bit được chia thành 16byte, có thể xếp thành 4 cột, mỗi cột 4 phần tử hay một ma trận 4x4 của các byte, nó gọi là ma trận trạng thái.
• Tùy thuộc vào độ dài của khóa khi sử dụng 128bit, 192bit hay 256bit mà thuật toán được thực hiện với số lần lặp khác nhau.

2. Các bước xử lý chính.

• Quá trình mở rộng khóa sử dụng thủ tục sinh khóa Rijndael.
• Quá trình mã hóa.

1. Xây dựng bảng S-box.

a. Bảng S – box thuận.

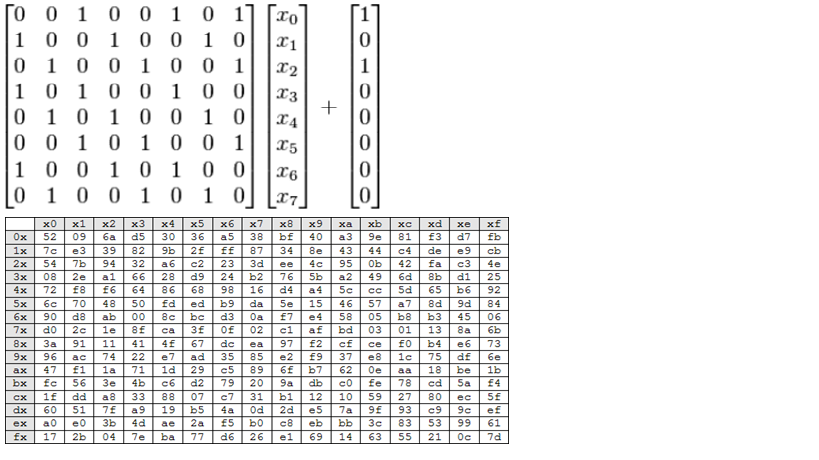
• Bảng S-box thuận được sinh ra bằng việc xác định nghịch đảo cho một giá trị nhất định trên GF(28) = GF(2)[x] / (x8+x4+x3+x+1) (trường hữu hạn Rijindael). Giá trị 0 không có nghịch đảo thì được ánh xạ với 0. Những nghịch đảo được chuyển đổi thông qua phép biến đổi affine.
• Công thức tính các giá trị bảng S-box và bảng S- box tương ứng:

b. Bảng S-box nghịch đảo.

• S-box nghịch đảo chỉ đơn giản là S-box chạy ngược. Nó được tính bằng phép biến đổi affine nghịch đảo các giá trị đầu vào. Phép biến đổi affine nghịch đảo được biểu diễn như sau:

2. Giải thuật sinh khóa phụ.

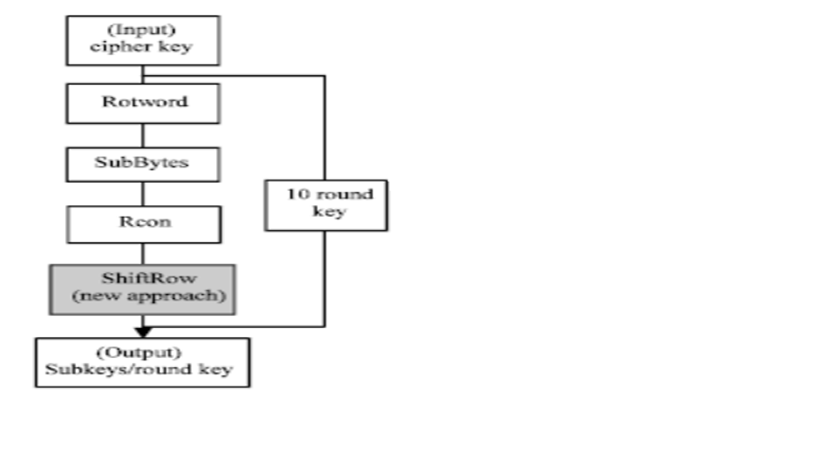
Quá trình sinh khóa gồm 4 bước:

• Rotword: quay trái 8 bít
• SubBytes
• Rcon: tính giá trị Rcon(i) Trong đó :

  Rcon(i) = x(i-1) mod (x8 + x4 + x3 + x + 1).
  

• ShiftRow

3. Quá trình mã hóa.

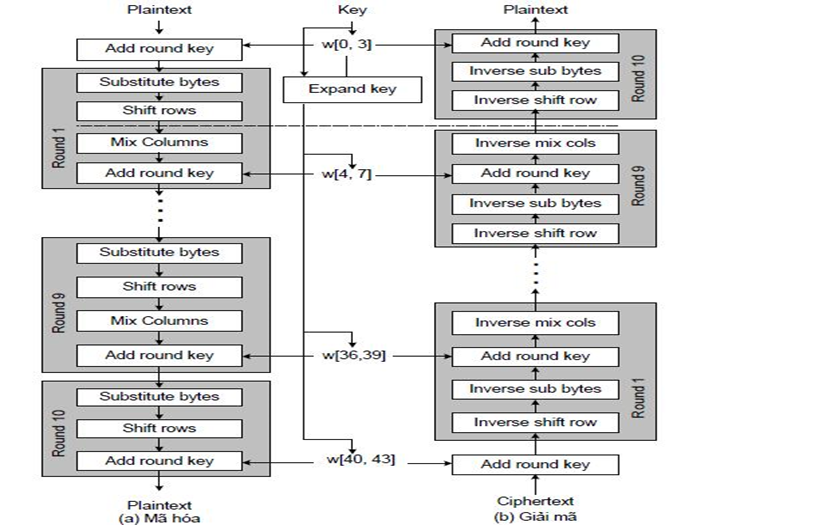
a. Sơ đồ tổng quát.

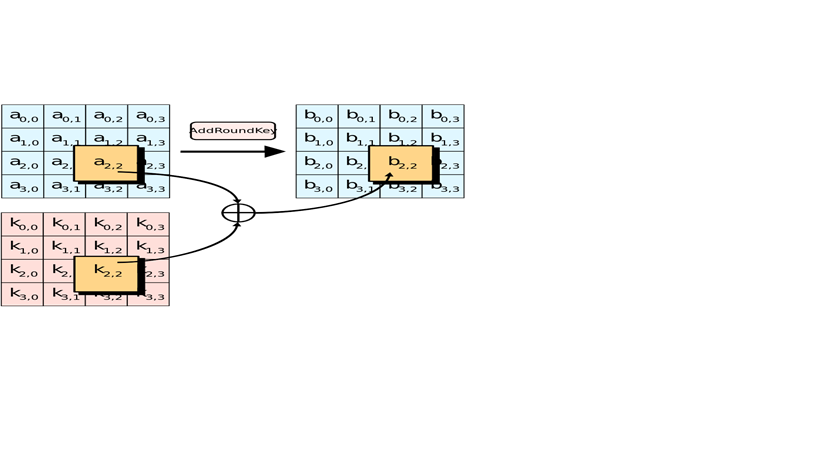
b. Hàm AddRoundKey.

• Được áp dụng từ vòng lặp thứ 1 tới vòng lặp Nr
• Trong biến đổi Addroundkey(), một khóa vòng được cộng với state bằng một phép XOR theo từng bit đơn giản.
• Mỗi khóa vòng gồm có 4 từ (128 bit) được lấy từ lịch trình khóa. 4 từ đó được cộng vào mỗi cột của state, sao cho:

  [S’0,c, S’1,c, S’2,c, S’3,c ] = [S0,c, S1,c, S2,c, S3,c ]  [W(4*i + c)] với 0 <= c < 4. 
  

  

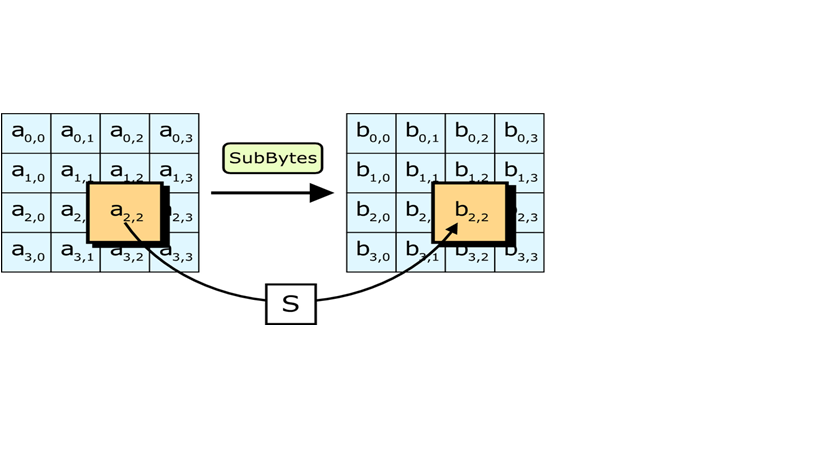
c. Hàm SubBytes.

• Biến đổi SubBytes() thay thế mỗi byte riêng rẽ của state Sr,c bằng một giá trị mới S’ r,c sử dụng bảng thay thế (S - box) được xây dựng ở trên.

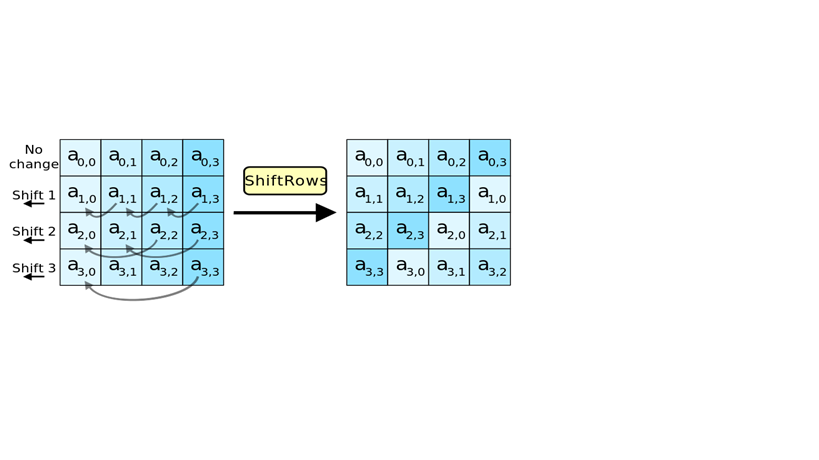
d. Hàm ShiftRow.

• Trong biến đổi ShiftRows(), các byte trong ba hàng cuối cùng của trạng thái được dịch vòng đi các số byte khác nhau (độ lệch). Cụ thể :

  S’r,c = Sr,(c + shift ( r, Nb)) mod Nb (Nb = 4)
  

• Trong đó giá trị dịch shift (r, Nb) phụ thuộc vào số hàng r như sau:

  Shift(1,4) = 1, shift(2,4) = 2, shift(3,4) = 3.
  

• Hàng đầu tiên không bị dịch, ba hàng còn lại bị dịch tương ứng:
  • Hàng thứ 1 giữ nguyên.
  • Hàng thứ 2 dịch vòng trái 1 lần.
  • Hàng thứ 3 dịch vòng trái 2 lần.
  • Hàng thứ 4 dịch vòng trái 3 lần.

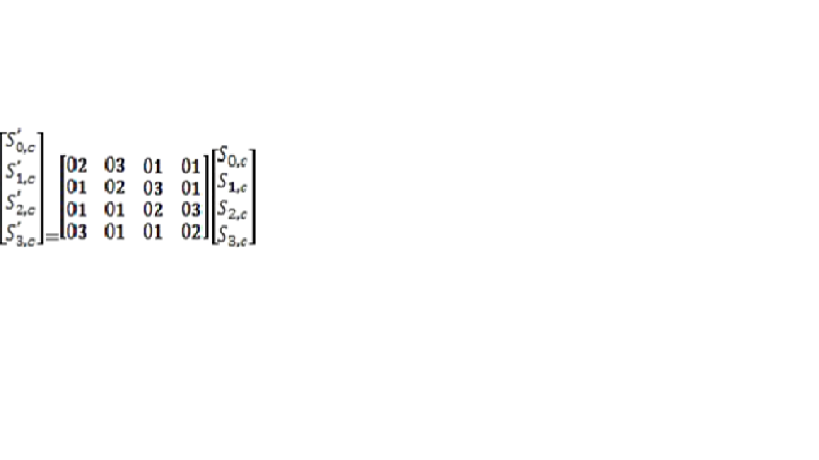
e. Hàm MixColumns.

• Biến đổi MixColumns() tính toán trên từng cột của state. Các cột được coi như là đa thức trong trường GF(28) và nhân với một đa thức a(x) với:

  a(x) = (03)x^3 +(01)x^2 +(01)x + (02)
  

• Biến đổi này có thể được trình bày như phép nhân một ma trận, mà mỗi byte được hiểu như là một phần tử trong trường GF(28): s’(x) = a(x)  s(x):
• Mô tả bằng ma trận như sau :

1. Tổng quan.

Thuật toán giải mã khá giống với thuật toán mã hóa về mặt cấu trúc nhưng 4 hàm sử dụng là 4 hàm ngược của quá trình mã hóa.

2. Thuật toán giải mã.

InvCipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)]) 
begin 
 
byte state[4,Nb] 
state = in
AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1]) 
for round = Nr-1 downto 1 
    InvShiftRows(state) 
    InvSubBytes(state) 
    AddRoundKey(state, w[round*Nb, (round+1)*Nb-1]) 
    InvMixColumns(state) 
end for 

InvShiftRows(state) 
InvSubBytes(state) 
AddRoundKey(state, w[0, Nb-1]) 
out = state 
end

Trong đó :

• In[] : Mảng dự liệu đầu vào Input.
• Out[] : Mảng dữ liệu đầu ra Output.
• Nr : Số vòng lặp.(Nr = 10).
• Nb : Số cột(Nb = 4).
• W[] : Mảng các w[i] có độ dài 4 bytes.

1. Side-channel attack.

• Side Channels (Kênh kề) được định nghĩa là các kênh đầu ra không mong muốn từ một hệ thống.
• Tấn công kênh bên hay còn gọi là Tấn công kênh kề là loại tấn công dễ thực hiện trong các loại tấn công mạnh chống lại quá trình triển khai mã hóa, và mục tiêu của loại tấn công này là phân tích các nguyên tố, các giao thức, modul, và các thiết bị trong mỗi hệ thống.
• Phân loại :
  • Tấn công thời gian.
  • Tấn công dựa vào lỗi.
  • Tấn công phân tích năng lượng.
  • Tấn công phân tích điện từ.

2. Known attacks.

• Vào năm 2002, Nicolas Courtois và Josef Pieprzyk phát hiện một tấn công trên lý thuyết gọi là tấn công XSL và chỉ ra điểm yếu tiềm tàng của AES.
• Tuy nhiên, một vài chuyên gia về mật mã học khác cũng chỉ ra một số vấn đề trong cơ sở toán học của tấn công này và cho rằng các tác giả đã có sai lầm trong tính toán. Việc tấn công dạng này có thực sự trở thành hiện thực hay không vẫn còn để ngỏ và cho tới nay thì tấn công XSL vẫn chỉ là suy đoán.

3. Các phương pháp phòng chống.

• Phương pháp 1: Mã hóa cực mạnh
  • Sử dụng các biện pháp để tăng tính bảo mật của các thuật toán mã hóa.
• Phương pháp 2: Bảo vệ dữ liệu theo phương pháp vật lý
  • Nếu một kẻ tấn công không thể tiếp cận vật lý với dữ liệu, dĩ nhiên khả năng đánh cắp khóa mã hóa sẽ khó khăn hơn. Vì vậy, trước những cuộc tấn công qua âm thanh tiềm tàng, bạn có thể sử dụng các giải pháp bảo vệ vật lý như đặt laptop vào các hộp cách ly âm thanh, không để ai lại gần máy tính khi đang giải mã dữ liệu hoặc sử dụng các nguồn âm thanh băng rộng tần số đủ cao để gây nhiễu.
• Phương pháp 3: Kết hợp cả 2 cách trên.

• Thiết kế và độ dài khóa của thuật toán AES ( 128, 192 và 256 bit ) là đủ an toàn để bảo vệ các thông tin được xếp vào loại tối mật nhưng về an ninh của AES thì các nhà khoa học đánh giá là chưa cao. Nếu các kỹ thuật tấn công được cải thiện thì AES có thể bị phá vỡ.
• Một vấn đề khác nữa là cấu trúc toán học của AES khá đơn giản.

• https://en.wikipedia.org/wiki/Advanced_Encryption_Standard