Ứng dụng thuật toán Naive Bayes trong giải quyết bài toán chuẩn đoán bệnh tiểu đường

Chào tất cả mọi người, đã rất lâu rồi mình mới có một bài Viblo mới viết về Machine Learning và hôm nay chúng ta sẽ đến với một phương pháp không phải là mới trong học máy nhưng vẫn luôn là một phương pháp đem lại hiệu quả tốt trong lớp các bài toán phân lớp hay dự đoán. Giải thuật mà chúng ta sẽ thảo luận ngày hôm nay chính là Naive Bayes - một trong những thuật toán rất tiêu biểu cho hướng phân loại dựa trên lý thuyết xác suất. Có một điều đặc biết trong bài Viblo này đó là phàn code mình sẽ không sử dụng thư viện Naive Bayes trong gói thư viện Scikit-learn quen thuộc như những bài Viblo trước mà thay vào đó mình sẽ hướng dẫn các bạn triển khai thuật toán này trên Python một cách step-by-step thông qua một ví dụ thực tế rất hay đó là chuẩn đoán bệnh nhận bị tiểu đường dựa vào những biểu hiện của người đó. OK chúng ta bắt đầu thôi nào.

Phương pháp học dựa trên xác suất

Nếu các bạn đã dõi các bài viết của mình về Machine Learning hoặc các tutorial khác về học máy thì có thể thấy được một điều rằng giữa Machine Learning và lý thuyết xác suất có một sự liên hệ rất khăng khít. Các phương pháp phân loại dựa trên lý thuyết xác suất về cơ bản có thể hiểu là việc tính xem xác suất một sự việc của chúng ta sẽ xảy ra theo hướng như thế nào. Xác suất của hướng nào càng cao thì khả năng sự việc xảy ra theo hướng đó càng nhiều. Điều này đặc biết có ý nghĩa trong bài toán dự đoán và phân lớp của lĩnh vực Machine Learning. Một câu hỏi đặt ra là ***Vậy rốt cuộc thì chiếc máy tính vô hồn của chúng ta sẽ xác định xác suất đó như thế nào ???***. Theo thống kê học hiện đại thì tương ứng với mỗi bài toán giải quyết theo phương pháp xác suất thường đi kèm theo một phân phối xác suất phù hợp với bài toán đó. Tương ứng với mỗi phân phối xác suất chúng ta có một cách tính riêng các đại lượng cần thiết cho quá trình chạy các thuật toán như kỳ vọng, độ lệch chuẩn ... mà chúng ta sẽ cùng nhau tìm hiểu và tiến hành tính toán trong suốt phạm vi bài viết này. Giờ thì chúng ta tiếp tục đến với phần tiếp theo thôi.

Thuật toán Naive Bayes

Lý thuyết Bayes thì có lẽ không còn quá xa lạ với chúng ta nữa rồi. Nó chính là sự liên hệ giữa các xác suất có điều kiện. Điều đó gợi ý cho chúng ta rằng chúng ta có thể tính toán một xác suất chưa biết dựa vào các xác suất có điều kiện khác. Thuật toán Naive Bayes cũng dựa trên việc tính toán các xác suất có điều kiện đó. Nghe tên thuật toán là đã thấy gì đó ngây ngô rồi. Tại sao lại là Naive nhỉ. Không phải ngẫu nhiên mà người ta đặt tên thuật toán này như thế. Tên gọi này dựa trên một giả thuyết rằng các chiều của dữ liệu $X=(x_1,x_2,....,x_n)$ là độc lập về mặt xác suất với nhau. Chúng ta có thể thấy rằng giả thuyết này có vẻ khá ngây thơ vì trên thực tế điều này có thể nói là không thể xảy ra tức là chúng ta rất ít khi tìm được một tập dữ liệu mà các thành phần của nó không liên quan gì đến nhau. Tuy nhiên, giả thiết ngây ngô này lại mang lại những kết quả tốt bất ngờ. Giả thiết về sự độc lập của các chiều dữ liệu này được gọi là Naive Bayes (xin phép không dịch). Cách xác định class của dữ liệu dựa trên giả thiết này có tên là Naive Bayes Classifier (NBC). Tuy nhiên dựa vào giả thuyết này mà bước training và testing trở nên vô cùng nhanh chóng và đơn giản. Chúng ta có thể sử dụng nó cho các bài toán large-scale. Trên thực tế, NBC hoạt động khá hiệu quả trong nhiều bài toán thực tế, đặc biệt là trong các bài toán phân loại văn bản, ví dụ như lọc tin nhắn rác hay lọc email spam. Trong bài viết này mình sẽ cùng với các bạn áp dụng lý thuyết về NBC để giải quyết một bài toán mới đó chính là bài toán chuẩn đoán bệnh tiểu đường

Tập dữ liệu bệnh tiểu đường

Tập dữ liệu này bao gồm dữ liệu của 768 tình nguyện viên bao gồm những người bị tiểu đường và những người không bị tiểu đường. Tập dữ liệu này bao gồm các thuộc tính như sau:

1. Number of times pregnant
2. Plasma glucose concentration a 2 hours in an oral glucose tolerance test
3. Diastolic blood pressure (mm Hg)
4. Triceps skin fold thickness (mm)
5. 2-Hour serum insulin (mu U/ml)
6. Body mass index (weight in kg/(height in m)^2)
7. Diabetes pedigree function
8. Age (years)

với mỗi tình nguyện viện, dữ liệu bao gồm tập hợp các chỉ số kể trên và tình trạng bị bênh tức class 1 hay không bị bệnh tức class 0. Về bản chất đây là một bài toán phân loại 2 lớp và chúng ta có thể sử dụng các phương pháp phân loại khác như SVM, Random Forest, kNN... để phân loại cũng cho kết quả khá tốt. Nếu có dịp mình sẽ trình bày phương pháp này trong một dịp khác. Chúng ta có thể hình dung tập dữ liệu này thông qua biểu diễn dưới dạng file CSV như sau, trong đó cột cuối cùng chính là tình trạng bị bệnh của tình nguyện viên, các cột từ 1 đến 8 tương ứng với các chỉ số nếu trên

Có một điều nhận thấy rằng giá trị của các chỉ số là một biến liên tục chứ không phải một giá trị rời rạc chính vì thế nên khi áp dụng thuật toán Naive Bayes chúng ta cần phải áp dụng một phân phối xác suất cho nó. Một trong những phân phối xác suất phổ biến được sử dụng trong phần này đó chính là phân phối Gaussian. Chúng ta cùng tìm hiểu qua một chút về nó nhé. Phải hiểu được bản chất thì mới có thể thực hành được.

Phân phối Gaussian

Với một một dữ liệu $x_i$ thuộc một class $c_i$ chúng ta thấy $x_i$ tuân theo một phân phối chuẩn với kì vọng $\mu$ và độ lệch chuẩn $\sigma$. Khi đó hàm xác suất của $x_i$ được xác định như sau:

$$p(x_i|c_i)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}\right)$$

Đây chính là cách tính của thư viện sklearn tuy nhiên trong bài viết này mình sẽ hướng dẫn các bạn cài đặt thủ công. Chính việc cài đặt thủ công này giúp cho chúng ta hiểu hơn về bài toán

Cài đặt thủ công

Load dữ liệu

Dữ liệu của chúng ta được lưu dưới dạng file CSV nên chúng ta sẽ sử dụng thư viện csv của Python để đọc dữ liệu

# Load data tu CSV file
def load_data(filename):
   lines = csv.reader(open(filename, "rb"))
   dataset = list(lines)
   for i in range(len(dataset)):
       dataset[i] = [float(x) for x in dataset[i]]

   return dataset

Tính độ lệch chuẩn

Như đã trình bày phần trên chúng ta cần một đoạn code để tính độ lệch chuẩn của biến ngẫu nhiên liên tục. Chúng ta có thể tham khảo công thức tính của nó như biểu thức sau:

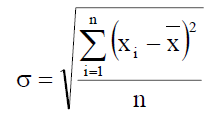
Trong đó $\overline{x}$ là gía trị trung bình của biến ngẫu nhiên trên toàn tập dữ liệu. Chúng ta sử dụng Python để thực hiện hàm tính giá trị trung bình và độ lệch chuẩn như sau

# tinh toan gia tri trung binh cua moi thuoc tinh
def mean(numbers):
    return sum(numbers) / float(len(numbers))

# Tinh toan do lech chuan cho tung thuoc tinh
def standard_deviation(numbers):
    avg = mean(numbers)
    variance = sum([pow(x - avg, 2) for x in numbers]) / float(len(numbers) - 1)

    return math.sqrt(variance)

Tiền xử lý dữ liệu

Trước khi bắt đầu mỗi bài toán về Machine Learning bước tiền xử lý dữ liệu là rất quan trọng. Nếu như tập dữ của chúng ta chưa chuẩn chúng ta sẽ cần phải làm thêm một số bước khác như lấy mẫu dữ liệu, loại bỏ dữ liệu thiếu và biến đổi dữ liệu về dạng thích hợp để xử lý.. Đối với tập dữ liệu bênh tiểu đường thì dữ liệu đã được chuẩn hóa rồi nên tùy vào từng thuật toán mà chúng ta chọn cách biểu diễn dữ liệu cho phù hợp. Như phần trên đã nói chúng ta sẽ sử dụng Độ lệch chuẩn và giá trị trung bình để tính toán các xác suất cần thiết nên cần có một hàm để chuyển đổi dữ liệu ban đầu về dạng tập hợp của độ lệch chuẩn và trung bình nhằm phục vụ cho các phép tính xác suất sau này.

# Chuyen ve cap du lieu  (Gia tri trung binh , do lech chuan)

def summarize(dataset):
    summaries = [(mean(attribute), standard_deviation(attribute)) for attribute in zip(*dataset)]
    del summaries[-1]

    return summaries

def summarize_by_class(dataset):
    separated = separate_data(dataset)
    summaries = {}
    for classValue, instances in separated.iteritems():
        summaries[classValue] = summarize(instances)

    return summaries

Tính xác suất của từng biến liên tục theo phân phối Gausian

Dựa vào cơ sở lý thuyết ở bên trên. Chúng ta tiến hành tính các xác suất phụ thuộc của biến ngẫu nhiên bao gồm $p(x)$ của mỗi chỉ số sức khỏe và $p(x|c)$ của mỗi class tương ứng với chỉ số đó.

# Tinh toan xac suat theo phan phoi Gause cua bien lien tuc the hien cac chi so suc khoe
def calculate_prob(x, mean, stdev):
    exponent = math.exp(-(math.pow(x - mean, 2) / (2 * math.pow(stdev, 2))))

    return (1 / (math.sqrt(2 * math.pi) * stdev)) * exponent

# Tinh xac suat cho moi chi so suc khoe theo class
def calculate_class_prob(summaries, inputVector):
    probabilities = {}
    for classValue, classSummaries in summaries.iteritems():
        probabilities[classValue] = 1
        for i in range(len(classSummaries)):
            mean, stdev = classSummaries[i]
            x = inputVector[i]
            probabilities[classValue] *= calculate_prob(x, mean, stdev)

    return probabilities

Dự đoán dựa vào xác suất

Đây là bước áp dụng định lý Bayes đã đước giới thiệu bên trên vào dự đoán các class thông qua các chỉ số trong tập dữ liệu

# Du doan vector thuoc phan lop nao
def predict(summaries, inputVector):
    probabilities = calculate_class_prob(summaries, inputVector)
    bestLabel, bestProb = None, -1
    for classValue, probability in probabilities.iteritems():
        if bestLabel is None or probability > bestProb:
            bestProb = probability
            bestLabel = classValue

    return bestLabel

# Du doan tap du lieu testing thuoc vao phan lop nao
def get_predictions(summaries, testSet):
    predictions = []
    for i in range(len(testSet)):
        result = predict(summaries, testSet[i])
        predictions.append(result)

    return predictions

# Tinh toan do chinh xac cua phan lop
def get_accuracy(testSet, predictions):
    correct = 0
    for i in range(len(testSet)):
        if testSet[i][-1] == predictions[i]:
            correct += 1

    return (correct / float(len(testSet))) * 100.0

Learning

Sau bước xử lý dữ liệu ban đầu chúng ta tiến hành learning như sau:

def main():
    filename = 'tieu_duong.csv'
    splitRatio = 0.8
    dataset = load_data(filename)
    trainingSet, testSet = split_data(dataset, splitRatio)

    print('Data size {0} 
Training Size={1} 
Test Size={2}').format(len(dataset), len(trainingSet), len(testSet))

    # prepare model
    summaries = summarize_by_class(trainingSet)

    # test model
    predictions = get_predictions(summaries, testSet)
    accuracy = get_accuracy(testSet, predictions)
    print('Accuracy of my implement: {0}%').format(accuracy)

Kết quả cài đặt

Sau khi cài đặt ta nhận thấy thuật toán tính toán rất nhanh và cho độ chính xác khoảng 75% tùy thuộc vào cách phân chia dữ liệu. Tiếp theo để kiểm tra cài đặt của thuật toán đã đúng chưa. Mình sẽ thử nghiệm so sánh với thư viện sklearn trong phần tiếp theo

Sử dụng thư viện Sklearn

Phân chia dữ liệu

Đầu tiên ta cần phân chia tập dữ liệu ban đầu thành hai ma trận, 1 ma trận chứa chỉ số của tình nguyện viên chính là 8 chỉ số đã chỉ ra ở phần đầu tiên và một ma trận chứa các class tương ứng.

def get_data_label(dataset):
    data = []
    label = []
    for x in dataset:
        data.append(x[:8])
        label.append(x[-1])

    return data, label

Training

Chúng ta thêm vào phần hàm $main()$ bên trên đoạn code sau để thực hiện training sử dụng thư viện

# Compare with sklearn
dataTrain, labelTrain = get_data_label(trainingSet)
dataTest, labelTest = get_data_label(testSet)

from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
clf.fit(dataTrain, labelTrain)

Predict

Sau khi training xong chúng ta sẽ sử dụng model để đánh giá trên tập dữ liệu testing.

score = clf.score(dataTest, labelTest)
print('Accuracy of sklearn: {0}%').format(score*100)

So sánh hai cách cài đặt

Sau khi chạy thử nghiệm cho kết quả giống nhau chứng tỏ cách cài đặt thủ công của chúng ta đã chính xác

Source code

Các bạn có thể tham khảo source code trong bài viết tại đây

Kết luận

Chúng ta đã cùng nhau đi qua một chặng đường dài tự lý thuyết xác suất đến thuật toán Naive Bayes rồi ứng dụng nó trong bài toán phần loại bệnh nhân mắc bệnh tiểu đường. Vấn đề của chúng ta rõ ràng vẫn là thống kê được những mối liện hệ và tìm được những xác suất của nó với vấn đề mà chúng ta quan tâm (ở đây chính là việc có bị tiểu đường hay không). Tuy độ chính xác còn chưa cao do bản chất cuả phương pháp cũng như tập dữ liệu chưa đủ lớn tuy nhiên nó cũng giúp bạn đọc hình dung được cách cài đặt thuật toán Naive Bayes