Ứng dụng xử lý ảnh trong thực thế với thư viện OpenCV C/C++(Các phép toán hình thái học trong ảnh)
I. Phép toán giãn nở (dilation) Phép toán giãn nở được được định nghĩa ⊕ = ⋃ ớ ⊂ trong đó, A là đối tượng trong ảnh, B là một cấu trúc phần tử ảnh. Phép toán này có tác dụng làm cho đối tượng ban đầu trong ảnh tăng lên về kích thước (giản nở ra). Cấu trúc phần tử ảnh (image ...
I. Phép toán giãn nở (dilation)
Phép toán giãn nở được được định nghĩa ⊕ = ⋃ ớ ⊂ trong đó, A là đối tượng trong ảnh, B là một cấu trúc phần tử ảnh. Phép toán này có tác dụng làm cho đối tượng ban đầu trong ảnh tăng lên về kích thước (giản nở ra).
Cấu trúc phần tử ảnh (image structuring element) là một hình khối được định nghĩa sẵn nhằm tương tác với ảnh xem nó có thỏa mãn một số tính chất nào đó không, một số cấu trúc phần tử hay gặp là cấu trúc theo khối hình vuông và hình chữ thập. Phép giãn nở trên ảnh nhị phân (Binary operator)
Công thức
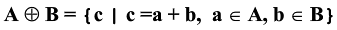
Trong đó:
A: Ma trận điểm ảnh của ảnh nhị phân.
B: Là phần tử cấu trúc. Phép giãn nở (Dilation) ảnh sẽ cho ra một tập điểm ảnh c thuộc D(i), bạn hoàn toàn dễ dàng thấy rằng đây là một phép tổng giữa A và B.
A sẽ là tập con của D(i) . Chú ý: Nhận xét này không toàn toàn đúng với trường hợp phần tử cấu trúc B không có gốc (Origin) hay nói cách khác là gốc (Origin) mang giá trị 0.
Ví dụ
- Tôi có ma trận điểm ảnh Isrc, ma trận điểm ảnh sau phép giãn nở Idst và phần tử cấu trúc B.
- Ứng với công thức ở trên, ta lần lượt đặt phần tử cấu trúc vào các điểm ảnh có giá trị 1 của ma trận điểm ảnh Isrc. Kết quả thu được là ma trận điểm ảnh Idst.
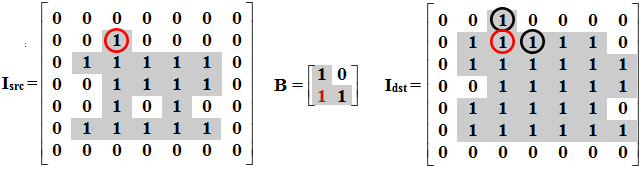
Tính toán
- Tôi có ở ma trận điểm ảnh Isrc = {(1, 2), (2,1), (2, 2), (2, 3), (2, 4), (2, 5), (3, 2), (3, 3), (3, 4), (3, 5), (4, 2), (4, 4), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5)}.
- Tôi có ở ma trận phần tử cấu trúc B = {(0,0), (-1, 0), (0, 1)} với (0,0) là điểm gốc.
Áp dụng công thức phép giãn nở tôi có:
- Isrc(0,0) = {(1, 2), (2,1), (2, 2), (2, 3), (2, 4), (2, 5), (3, 2), (3, 3), (3, 4), (3, 5), (4, 2), (4, 4), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5)}.
- Isrc(-1,0) = {(0, 2), (1,1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5)}.
- Isrc(0, 1) = {(1, 3), (2,2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6), (4, 3), (4, 5), (5, 3), (5, 3), (5, 4), (5, 5), (5, 6)}
Phép giãn nở của Isrc bởi B là hợp của Isrc(0,0), Isrc(-1,0) và Isrc(0,1) hay là Idst. Với phần tử cấu trúc không có điểm gốc (Origin), cách tính toán cũng tương tự.
II.Phép giãn nở trên ảnh đa mức xám (Grayscale dilation)
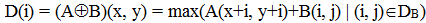
Trong đó
- A: Ma trận điểm ảnh của ảnh xám.
- B: Là phần tử cấu trúc.
- DB: Là không gian ảnh của phần tử cấu trúc không phẳng B.
III.Phép toán co (Erosion)
Phép toán co (Erosion) là một trong hai hoạt động cơ bản (khác phép giãn nở) trong hình thái học có ứng dụng trong việc giảm kích thước của đối tượng, tách rời các đối tượng gần nhau, làm mảnh và tìm xương của đối tượng.
*Phép co trên ảnh nhị phân (Binary operator)
Công thức
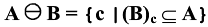
Trong đó:
- A: Ma trận điểm ảnh của ảnh nhị phân.
- B: Là phần tử cấu trúc.
Phép co ảnh sẽ cho ra một tập điểm ảnh c thuộc A, nếu bạn đi chuyển phần tử cấu trúc B theo c, thì B nằm trong đối tượng A. E(i) là một tập con của tập ảnh bị co A. Chú ý: Nhận xét này không toàn toàn đúng với trường hợp phần tử cấu trúc B không có gốc (Origin) hay nói cách khác là gốc (Origin) mang giá trị 0.
IV.Phép toán mở (Opening) và phép toán đóng (Closing)
Phép toán mở (Opening) và phép toán đóng (Closing) là sự kết hợp của phép co (Erosion) và phép giãn nở (Dilation) như trên. Ta được định nghĩa như sau.
1.Phép toán mở (Opening)
Thực hiện phép co (Erosion) trước sau đó mới thực hiện phép giãn nở (Dilation).
Công thức
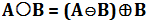
Ứng dụng
Phép toán mở (Opening) được ứng dụng trong việc loại bỏ các phần lồi lõm và làm cho đường bao các đối tượng trong ảnh trở nên mượt mà hơn.
2.Phép toán đóng (Closing)
Thực hiện phép giãn nở (Dilation) trước sau đó mới thực hiện phép co (Erosion).
Công thức
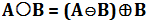
Ứng dụng
Phép toán đóng (Closing) được dùng trong ứng dụng làm trơn đường bao các đối tượng, lấp đầy các khoảng trống biên và loại bỏ những hố nhỏ.
V.Các phép toán hình thái học trong OpenCV
Trong OpenCV, các phép toán hình thái học trong ảnh được cài đặt trong hàm cv::morphologyEx().
cv::morphologyEx( InputArray src, OutputArray dst, int op, InputArray kernel,
Point anchor = Point(-1,-1), int iterations = 1,
int borderType = BORDER_CONSTANT,
const Scalar& borderValue = morphologyDefaultBorderValue());
Phân tích
- src: Là ảnh ban đầu:
- dst: Là ảnh sau khi xử lý hình thái học.
- op: Là loại hình thái học, ví dụ: MORPH_ERODE. Bạn có thể tham kháo các loại phép toán hình thái học trong cv::MorphTypes.
- kernel: Là phần tử cấu trúc. Bạn hoàn toàn có thể khởi tạo và sử dụng bằng cách sử dụng hàm getStructuringElement().
- anchor: Là điểm neo của phần tử cấu trúc kernel. Giá trị mặc định là (-1, -1).
- iterations: Số lần lặp đi lặp lại các phép toán hình thái học lên ảnh. Ví dụ: Bạn càng để phép toán giãn nở ảnh (Dialation) thì ảnh càng giãn nở nhiều.
- borderType-borderValue: Là giới hạn biên của những điểm ảnh (Pixel) nằm ngoài kích thước của ảnh trong quá trình tính toán.
Hàm getStructuringElement():
cv::getStructuringElement(int shape, Size ksize, Point anchor = Point(-1,-1));
Phân tích
- shape: Là hình dạng của phần tử cấu trúc. Ví dụ: MORPH_RECT. Bạn có thể tham khảo các loại hình dạng của phần tử cấu trúc trong cv::MorphShapes.
- ksize: Là kích thước của ma tận phần tử cấu trúc.
- anchor: Là điểm neo của phần tử cấu trúc. Giá trị mặc định là (-1, -1).
Ví Dụ
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
using namespace cv;
int main() {
Mat imageSrc = imread("stdio.png", CV_LOAD_IMAGE_GRAYSCALE);
Mat imageDst;
Mat imageBinary;
threshold(imageSrc, imageBinary, 220, 255, CV_THRESH_BINARY);
cv::Mat kernel = cv::getStructuringElement(MORPH_CROSS, Size(5,5));
cv::morphologyEx(imageBinary, imageDst, MORPH_ERODE, kernel);
imshow("imageBinary", imageBinary);
imshow("imageDst", imageDst);
waitKey(0);
return 0;
}
