Xác suất và Thống kê với NumPy - ài liệu học Numpy từ cơ bản đến nâng cao

Có khi nào bạn tự hỏi rằng dự báo thời tiết trên VTV mỗi ngày làm thế nào để đoán được thời tiết trong tuần tới? Câu trả lời là người ta đã xây dựng các mô hình trên máy tính sử dụng số liệu thống kê những dữ liệu thời tiết trong quá khứ và hiện tại để dự báo xác suất xảy ra các hiện tượng trong tương lai.

NumPy hỗ trợ khá nhiều hàm hỗ trợ thống kê cũng như xác suất. Sau khi đã làm quen với các thao thác tính toán trên mảng ở bài 4 cũng như cơ chế broadcasting thì ở bài này, ta sẽ cùng nhau tìm hiểu cơ chế cũng như cách sử dụng các hàm đó. Nếu bạn đã làm quen với toán Thống kê ở Đại học thì bài này sẽ khá là đơn giản, còn không thì đừng lo, mình sẽ giải thích chi tiết về các công thức toán một cách dễ hiểu nhất.

1. Thống kê

Giá trị trung tâm (Central Tendency)

Tính toán giá trị trung tâm cho ta biết một giá trị điển hình trong tập dữ liệu. Có 2 kiểu đánh giá chính mà ta cần quan tâm là mean (trung bình), median (trung vị).

Mean (Trung bình)

Đây là một trong những phương pháp đo khá quen thuộc, giả sử ta có dãy số sau:

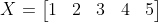
Thì mean chính là giá trị trung bình của dãy số này:

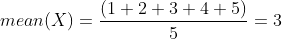
Trong NumPy ta tính mean của dãy số trên như với cú pháp

import numpy as np

X = [1, 2, 3, 4, 5]
print("Mean X = ", np.mean(X))

Mean X =  3.0

Tương tự với nhiều hàm tính toán, ta có thể tính mean theo từng trục nếu là mảng nhiều chiều:

X = np.array([[1, 2], [3, 4]])
print("Mean X = ", np.mean(X))
print("Mean X với axis = 0: ", np.mean(X, axis=0))
print("Mean X với axis = 1: ", np.mean(X, axis=1))

Mean X =  2.5
Mean X với axis = 0:  [2. 3.]
Mean X với axis = 1:  [1.5 3.5]

Lưu ý là với định dạng single precision (float32), mean có thể không chính xác với các mảng lớn:

a = np.zeros((2, 512*512), dtype=np.float32)
a[0, :] = 1.0
a[1, :] = 0.1


print("a.shape: ", a.shape)
print("mean a = ", np.mean(a))

Sử dụng double precision (float64) sẽ chính xác hơn:

print("mean a = ", np.mean(a, dtype=np.float64))

mean a =  0.5500000007450581

Median (trung vị)

Median (trung vị) là giá trị trung tâm của một dãy số với điều kiện là dãy số đó phải sắp xếp theo thứ tự từ bé đến lớn. Để tìm median thì sẽ có 2 trường hợp:

Với dãy có số lượng phần tử là số lẻ, chẳng hạn dãy sau có 5 phần tử

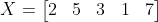
Để tìm mean của X, đầu tiên ta sẽ sắp xếp dãy theo thứ tự từ bé đến lớn:

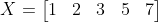
Và mean của dãy chính là phần tử nằm giữa dãy số:

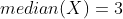
Với dãy có số lượng phần tử là số chẵn, như dãy sau có 6 phần tử:

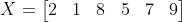
Dãy sau khi sắp xếp lại:

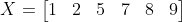
Ở đây ta thấy chính giữa dãy có 2 phần tử là 5 và 7, thì median của dãy chính là trung bình của 2 số đó:

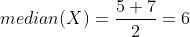
Median được tính bằng NumPy như sau:

X = np.array([2, 5, 3, 1, 7])
Y = np.array([2, 1, 8, 5, 7, 9])

print("Median X = ", np.median(X))
print("Median Y = ", np.median(Y))

Median X =  3.0
Median Y =  6.0

Tương tự như mean, median có thể tính theo các trục với mảng nhiều chiều:

arr = np.array([[7, 4, 2], [3, 9, 5]])
print("median arr (axis = 0) = ", np.median(arr, axis=0))
print("median arr (axis = 1) = ", np.median(arr, axis=1))

median arr (axis = 0) =  [5.  6.5 3.5]
median arr (axis = 1) =  [4. 5.]

Mean được sử dụng chủ yếu khi tập dữ liệu phân bố khá đồng đều với nhau, chẳng từ tập dữ liệu số người truy cập Zaidap.com trong vòng 1 tuần qua như sau, ta có tính được trung bình mỗi ngày có bao nhiêu người truy cập Zaidap.com:

Zaidap.com_visitors = np.array([3776, 3112, 3476, 3319, 3559, 2121, 3462])
print("Số người truy cập trung bình mỗi ngày trong tuần qua của Zaidap.com: ", np.mean(Zaidap.com_visitors))

Số người truy cập trung bình mỗi ngày trong tuần qua của Zaidap.com:  3260.714285714286

Tuy nhiên, nếu như phân phối bị lệch thì mean lúc này sẽ không còn nhiều ý nghĩa nữa, lúc đó ta sẽ dùng median, chẳng hạn:

Zaidap.com_visitors = np.array([3776, 3112, 3476, 3319, 3559, 50293, 30432]) # 2 giá trị cuối lệch xa so với các giá trị trong dãy
print("Mean = : ", np.mean(Zaidap.com_visitors))
print("Median = : ", np.median(Zaidap.com_visitors))

Mean = :  13995.285714285714
Median = :  3559.0 # Median cho giá trị biểu thị tốt hơn

Xử lý nan trong mean và median

Để bỏ qua các phần tử có giá trị nan trong mảng khi tính mean và median, NumPy cung cấp cho ta 2 hàm sau:

x = np.array([2, np.nan, 5, 9])
print("mean = ", np.nanmean(x))
print("median = ", np.nanmedian(x))

mean =  5.333333333333333
median =  5.0

Nếu như sử dụng mean và median thông thường thì kết quả trả về sẽ là nan:

print("mean = ", np.mean(x))
print("median = ", np.median(x))

mean =  nan
median =  nan

Phương sai và Độ lệch chuẩn (Variance & Standard Deviation)

Phương sai là là phép đo mức chênh lệch giữa các số liệu trong một tập dữ liệu trong thống kê. Nó đo khoảng cách giữa mỗi số liệu với nhau và đến giá trị trung bình của tập dữ liệu. Độ lệch chuẩn là căn bậc hai của phương sai.

Công thức tính phương sai:

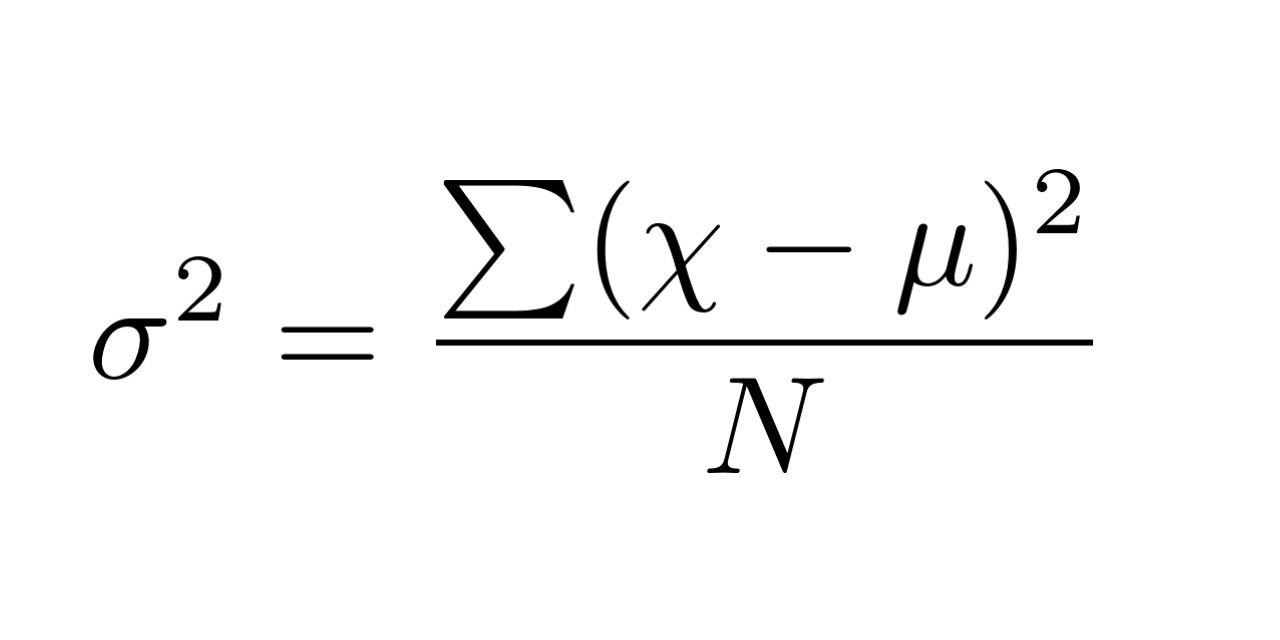
Ta sẽ đi đến một ví dụ để dễ hiểu hơn, giả sử ta có dãy X sau:

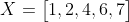
Đầu tiên ta đi tìm trung bình của dãy này:

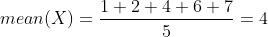
Lấy từng giá trị của X trừ đi mean (chênh lệch) sẽ có dãy sau:

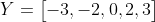
Để tính phương sai, ta lấy bình phương từng phần tử trên, sau đó tính trung bình:

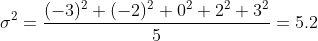
Và để tính độ lệch chuẩn, ta chỉ cần căn bậc hai giá trị của phương sai:

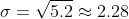
Sau khi ta đã biết được cách tính phương sai và độ lệch chuẩn trong toán, ta sẽ tìm hiểu cách tính trong NumPy và ứng dụng của nó.

Giả sử ta có mảng sau chứa các phần tử là tuổi của các cộng tác viên tại Zaidap.com.net:

Zaidap.com_ages = [19, 33, 51, 22, 18, 13, 45, 24, 58, 11, 25, 27, 26, 29]

Để tính phương sai và độ lệch chuẩn thì NumPy hỗ trợ 2 hàm sau:

Zaidap.com_ages = [19, 33, 51, 22, 18, 13, 45, 24, 58, 11, 25, 27, 26, 29]

print("Phương sai: ", np.var(Zaidap.com_ages))
print("Độ lệch chuẩn: ", np.std(Zaidap.com_ages))

Phương sai:  178.51530612244895
Độ lệch chuẩn:  13.360962020844493

Dựa vào độ lệch chuẩn và giá trị trung bình ta có biểu đồ sau:

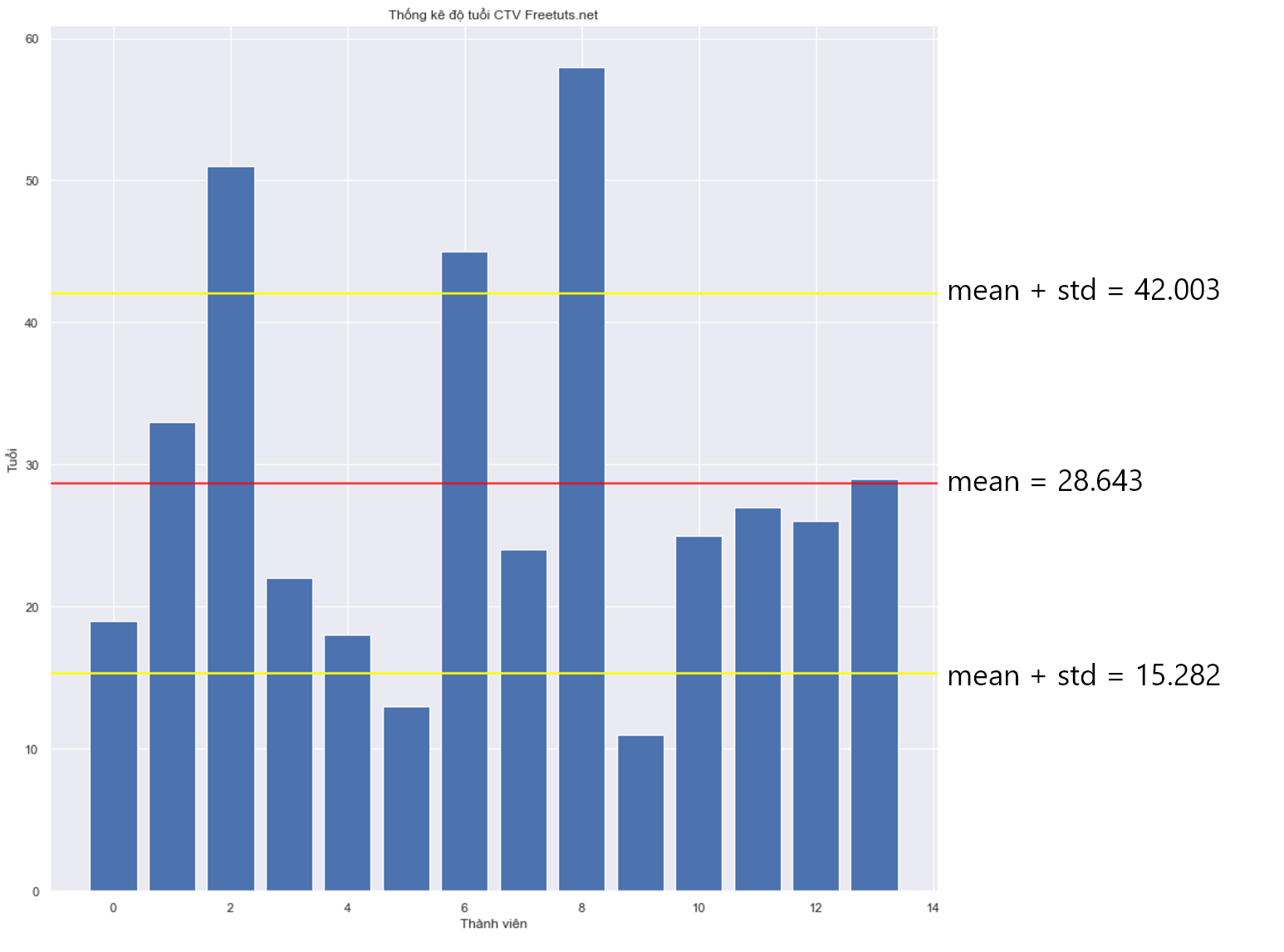
Từ khoảng chênh lệch giữa độ lệch chuẩn và giá trị trung bình, ta có thể biết được khoảng giá trị nào là "ổn định" và khoảng nào thì quá lớn hoặc quá nhỏ. Như trong biểu đồ trên, ta thấy độ tuổi từ 15 - 42 là "chuẩn", còn các độ tuổi như 11, 13 hay 45, 51 là quá nhỏ và quá lớn.

Xử lý nan trong var và std

Tuơng tự như mean và median, NumPy cũng cho chúng ta các hàm để bỏ qua các phần tử nan như sau:

a = np.array([1, np.nan, 3, 4])
print("var = ", np.var(a))
print("std = ", np.std(a))
print("nanvar = ", np.nanvar(a))
print("nanstd = ", np.nanstd(a))

var =  nan
std =  nan
nanvar =  1.5555555555555554
nanstd =  1.247219128924647

Thống kê thứ tự (Order statistics)

Giá trị lớn nhất và nhỏ nhất

x = np.array([[14, 96],
               [46, 82],
               [80, 67],
               [77, 91],
               [99, 87]])

print("X = ", x)

print("Giá trị lớn nhất: ", np.amax(x))
print("Giá trị bé nhất: ", np.amin(x))

print("Giá trị lớn nhất (axis = 0): ", np.amax(x, axis=0))
print("Giá trị lớn nhất (axis = 1): ", np.amax(x, axis=1))

X =  [[14 96]
 [46 82]
 [80 67]
 [77 91]
 [99 87]]
Giá trị lớn nhất:  99
Giá trị bé nhất:  14
Giá trị lớn nhất (axis = 0):  [99 96]
Giá trị lớn nhất (axis = 1):  [96 82 80 91 99]

Để bỏ qua các phần tử nan:

x = np.array([[14, 96],
               [np.nan, 82],
               [80, 67],
               [77, np.nan],
               [99, 87]])

print("X = ", x)

print("Giá trị lớn nhất: ", np.nanmax(x))
print("Giá trị bé nhất: ", np.nanmin(x))

X =  [[14. 96.]
 [nan 82.]
 [80. 67.]
 [77. nan]
 [99. 87.]]
Giá trị lớn nhất:  99.0
Giá trị bé nhất:  14.0

Phạm vi giá trị (Range)

Phạm vi giá trị chính là max - min trong một dãy số. Ví dụ:

print("x = ", x)

print("Range = ", np.ptp(x))
print("Range (axis = 0) = ", np.ptp(x, axis=0))
print("Range (axis = 1) = ", np.ptp(x, axis=1))

x =  [[14 96]
 [46 82]
 [80 67]
 [77 91]
 [99 87]]
Range =  85
Range (axis = 0) =  [85 29]
Range (axis = 1) =  [82 36 13 14 12]

Bách phân vị (Percentiles) và Tứ phân vị (Quartiles)

Để tính vị trí tương đối của một giá trị so với các giá trị khác thì 2 phương pháp đo phổ biến nhất là điểm phần trăm (bách phân vị) và điểm phần tư (tứ phân vị).

Bách phân vị thứ p (pth percentile) đơn giản là chia một tập dữ liệu thành 100 phần bằng nhau, thì tại vị trí có p phần trăm trên tổng số quan sát nhận giá trị nhỏ hơn hoặc bằng giá trị tại điểm đó (dữ liệu đã được sắp xếp theo thứ tự từ nhỏ đến lớn).

Giả sử trong một bài kiểm tra, nếu có 200 người làm bài và bạn đạt được bách phân vị thứ 70 (70th percentiles) thì có nghĩa là bạn đạt được điểm cao hơn hoặc bằng 70% người làm số bài kiểm tra đó (140 người), cũng như có 30% (60 người) đạt điểm cao hơn bạn.

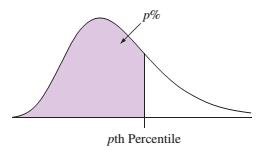
Trong NumPy thì tìm bách phân vị được tính bởi hàm np.percentile(a, q, axis=None, iterpolation='linear'):

• a: Input array
• q: Điểm bách phân vị (0 <= q <= 100)
• axis: trục tương ứng
• iterpolation: phép nội suy, mặc định là 'linear', tham số tùy chọn này chỉ định phương pháp nội suy để sử dụng khi phân vị mong muốn nằm giữa hai điểm dữ liệu i và j. Có 5 kiểu nội suy NumPy hỗ trợ:
  • ​'linear' (nội suy tuyến tính): i + (j - i) * fraction với fraction là phần phân số của chỉ số được bao quanh bởi i và j
  • 'lower': i
  • 'higher': j
  • 'nearest': i hoặc j (chọn cái nào gần hơn)
  • 'midpoint': (i + j) / 2

Ví dụ:

scores = np.array([8, 6, 4, 3, 9, 4, 7, 4, 4, 9, 7, 3, 9, 4, 2, 3, 8, 5, 9, 6])

print("Bách phân vị thứ 70: ", np.percentile(scores, 70, interpolation='lower'))
print("Bách phân vị thứ 70: ", np.percentile(scores, 70, interpolation='higher'))
print("Bách phân vị thứ 70: ", np.percentile(scores, 70, interpolation='linear'))
print("Bách phân vị thứ 70: ", np.percentile(scores, 70, interpolation='nearest'))
print("Bách phân vị thứ 70: ", np.percentile(scores, 70, interpolation='midpoint'))

Bách phân vị thứ 70:  7
Bách phân vị thứ 70:  8
Bách phân vị thứ 70:  7.299999999999999
Bách phân vị thứ 70:  7
Bách phân vị thứ 70:  7.5

Ta nhớ lại khái niệm về trung vị (median) đã nói ở trên: trung vị là giá trị giữa của dãy số được sắp xếp từ bé đến lớn, vì vậy bách phân vị thứ 50 chính là median của dãy số đó:

print("Bách phân vị thứ 50: ", np.percentile(scores, 50))
print("Median = ", np.median(scores))

Bách phân vị thứ 50:  5.5
Median =  5.5

Tứ phân vị (Quartiles) chính là Bách phân vị được chia thành 3 phần (Q1 => Q3) bằng nhau, tương ứng với bách phân vị thứ 25 (Q1), thứ 50 (Q2), thứ 75 (Q3):

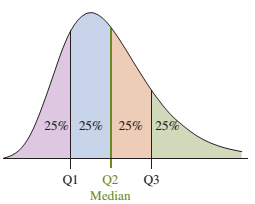
Trong NumPy thì tìm tứ phân vị được tính bởi hàm np.quantile(a, q, axis=None, iterpolation='linear'):

• a: Input array
• q: Điểm tứ phân vị (0 <= q <= 1)
• axis: trục tương ứng
• iterpolation: phép nội suy, tương tự như np.percentile

Ví dụ:

print("Q1 = : ", np.quantile(scores, 0.25))
print("Q2 = : ", np.quantile(scores, 0.5))
print("Q3 = : ", np.quantile(scores, 0.75))

Q1 = :  4.0
Q2 = :  5.5
Q3 = :  8.0

Cũng tương tự như những hàm khác, np.percentile và np.quantile cũng có 2 hàm tương ứng cho việc xử lý nan là np.nanpercentile và np.nanquantile

2. Xác suất

Giới thiệu về xác suất trong NumPy

Để tìm hiểu các hàm ngẫu nhiên phổ biến trong NumPy, ta sẽ cùng đi đến một bài toán quen thuộc trong xác suất mà hồi THPT đã học, đó là bài toán lật đồng xu: chúng ta có một đồng xu và muốn biết kết quả của một lần lật đồng xu là úp hay ngửa.

random.randint

Chúng ta sẽ sử dụng hàm np.random.randint để giải quyết bài toán, hàm nhận vào 2 tham số (số nguyên) chính là phạm vi trả về số ngẫu nhiên:

np.random.randint(0, 2) # Ngẫu nhiên số nguyên trong khoảng [0, 2)

0

Vì phạm vi là [0, 2) nên chỉ có 2 giá trị là 0 hoặc 1 sẽ được trả về. Mình sẽ gọi 0 là mặt ngửa, 1 là mặt úp. Ta thấy trong trường hợp trên đã nhận được mặt ngửa.

Giờ ta sẽ giả sử tung 1000 đồng xu bằng cách truyền vào tham số size:

coins = np.random.randint(2, size=1000) 
print(coins.shape)

(1000,)

Nếu ta tính % số lần tung được mặt ngửa và úp, ta sẽ thấy nó đều xấp xỉ 50%:

print("% số lần tung được mặt ngửa: ", (coins == 0).mean() * 100)
print("% số lần tung được mặt úp: ", (coins == 1).mean() * 100)

% số lần tung được mặt ngửa:  48.9
% số lần tung được mặt úp:  51.1

random.choice

Chúng ta có thể khiến cho một giá trị trở nên thiên vị (bias) bằng hàm np.random.choice, ví dụ ta muốn số mặt úp đạt 80% còn số mặt ngửa chỉ 20%:

coins = np.random.choice([0, 1], size=1000, p=[0.2, 0.8]) # random.choice sẽ lấy ngẫu nhiên các phần tử trong mảng ở tham số đầu tiên với xác suất ở tham số p
print("% số lần tung được mặt ngửa: ", (coins == 0).mean() * 100)
print("% số lần tung được mặt úp: ", (coins == 1).mean() * 100)

% số lần tung được mặt ngửa:  20.599999999999998
% số lần tung được mặt úp:  79.4

random.binomial

Nếu như chúng ta lật 10 đồng xu trong 1000 lần, thì xác suất nhận được 7 mặt ngửa là bao nhiêu?

Đây chính là trường hợp của "Binomial Distribution" (Phân phối nhị thức). Phân phối này là một phân phối xác suất tóm tắt khả năng để một giá trị lấy một trong hai giá trị độc lập trong một tập hợp các tham số hoặc giả định nhất định. NumPy hỗ trợ bài toán này bằng hàm np.random.binomial, hàm này thể hiện xác suất để x thành công trong n phép thử, với xác suất thành công p của mỗi phép thử.

• Với p = 0.5; phân phối sẽ cân đối quanh giá trị trung bình.
• Khi p > 0.5; phân phối sẽ lệch về bên trái.
• Và khi p < 0.5 phân phối sẽ lệch về bên phải.

Trong trường hợp đồng xu, “n” sẽ là số lần lật và “p” sẽ là xác suất thành công ( = 0.5):

np.random.binomial(20, 0.5) # Số mặt ngửa nhận được khi tung đồng xu 10 lần

9

Hoặc ta có thể tung đồng xu 20 lần trong 10 lần thử:

np.random.binomial(20, 0.5, 10) # Số mặt ngửa nhận được khi tung đồng xu 20 lần trong 10 lần lặp

array([10, 10,  9,  6, 10, 11, 13, 10,  8,  9])

Và ta có thể tìm được trung bình số mặt ngửa nhận được:

print("Trung bình số mặt ngửa nhận được khi tung đồng xu 20 lần trong vòng 10 lần lặp: ", np.random.binomial(20, 0.5, 10).mean())

Trung bình số mặt ngửa nhận được khi tung đồng xu 20 lần trong vòng 10 lần lặp:  10.4

Ở 2 trường hợp trên, dễ thấy ta đang dùng đồng xu không bị thiên vị (p=0.5) nên mới có được 10.4 mặt ngửa sau 20 lần tung (tương đương 50%). Ta có thể thêm bias vào như sau:

n = 10 # tung 10 đồng xu trong 1 lần
p = 0.2 # bias cho mặt ngửa (xác suất cho mặt ngửa là 0.2)
l = 1000 # số lần lặp

b = np.random.binomial(n, p, l)
print("Trung bình số mặt ngửa nhận được: ", b.mean())

Trung bình số mặt ngửa nhận được:  1.993 # Nhận 1.993 mặt ngửa sau 10 lần tung (~20%)

Có rất nhiều loại phân phối được hỗ trợ trong NumPy, bạn có thể tìm thêm ở đây: Random sampling (numpy.random) — NumPy v1.16 Manual

Xây dựng mảng ngẫu nhiên trong NumPy

Sau khi đã tìm hiểu về các hàm xác suất cơ bản, ta sẽ đến với các hàm tạo mảng ngẫu nhiên trong NumPy:

numpy.random.rand

Hàm numpy.random.rand trả về một mảng các số ngẫu nhiên mà mỗi phần tử là một số ngẫu nhiên có phân bố đều (uniform distribution) trong khoảng [0, 1):

a = np.random.rand()
b = np.random.rand(4) # Mảng có 1x8 phần tử
c = np.random.rand(2, 3) # Mảng có 2x3 phần tử

print("a = ", a)
print("b = ", b)
print("c = ", c)

a =  0.3421628209488957
b =  [0.46813023 0.08351749 0.45755406 0.39447444]
c =  [[0.07105495 0.33631271 0.88374921]
 [0.96496987 0.62399799 0.88844741]]

numpy.random.seed

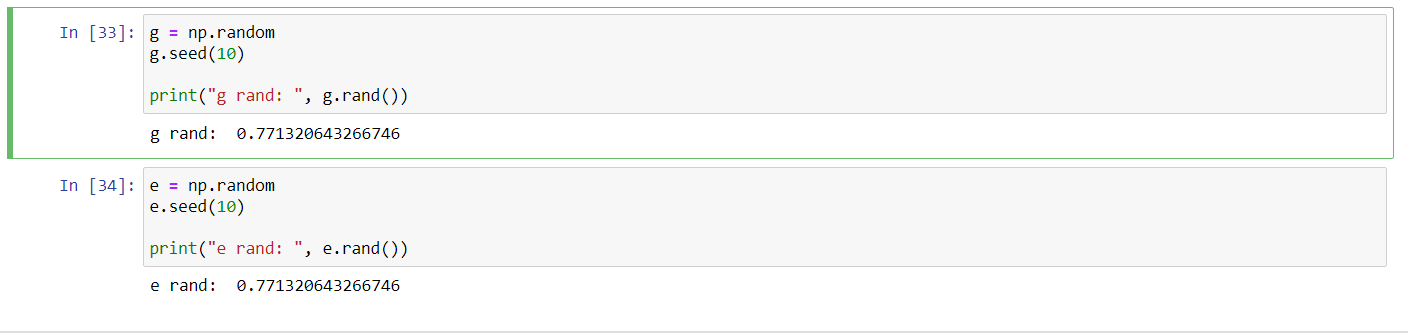
NumPy không thực sự tạo ra số ngẫu nhiên mà thực chất nó sử dụng bộ sinh số giả ngẫu nhiên (Pseudorandom number generator). Hàm numpy.random.seed là một hàm tạo các bộ sinh số ngẫu nhiên (random generator) và tham số thường là một số nguyên không âm, các giá trị của biến số khác nhau thì sẽ cho ra các số ngẫu nhiên khác nhau, và ngược lại, giống nhau thì sẽ ra số giống nhau, ví dụ:

g = np.random
g.seed(10)

print("g rand: ", g.rand())

g rand:  0.771320643266746

e = np.random
e.seed(10)

print("e rand: ", e.rand())

e rand:  0.771320643266746

numpy.random.normal

Phân phối chuẩn, còn gọi là phân phối Gauss hay (Hình chuông Gauss), là một phân phối xác suất cực kì quan trọng trong nhiều lĩnh vực. Nó là họ phân phối có dạng tổng quát giống nhau, chỉ khác tham số vị trí (giá trị trung bình μ - mean) và tỉ lệ (phương sai σ^2 - variance).

Đây là phương trình của phân phối:

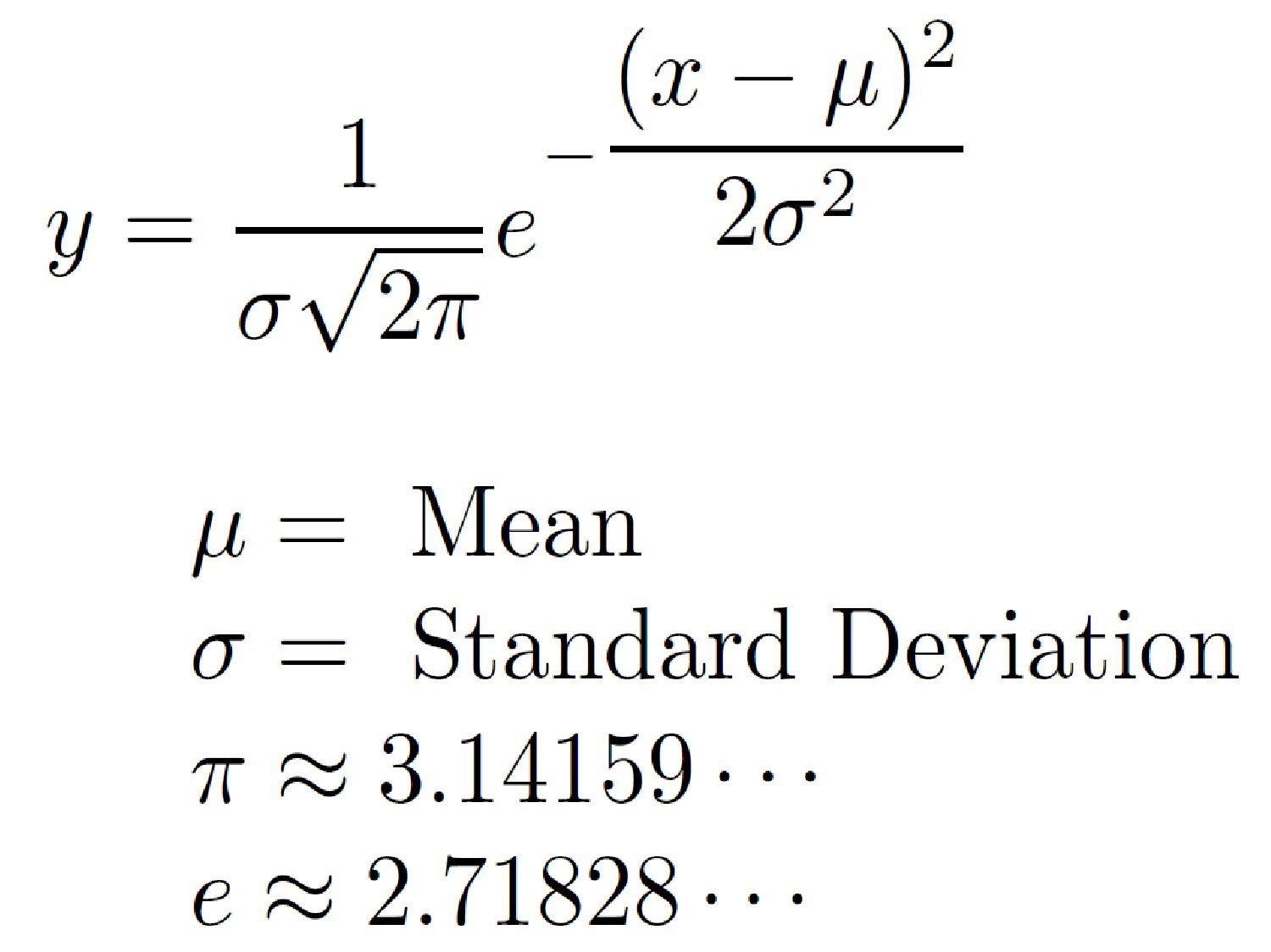
Đây là đồ thị "hình chuông" phổ biến biểu thị cho phân phối chuẩn:

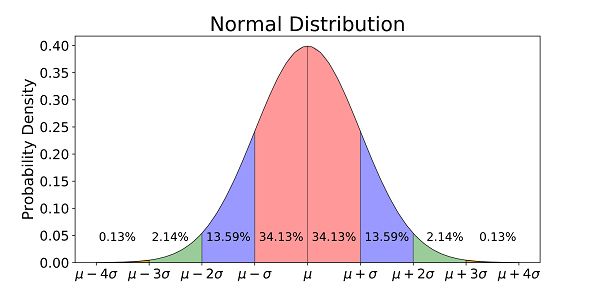
Phân phối chuẩn chi phối cuộc sống hằng ngày khá nhiều, ví dụ nếu như bạn xem phổ điểm Đại học các năm, sẽ để ý thấy gần như mọi môn đều có đồ thị dạng "chuông", chẳng hạn:

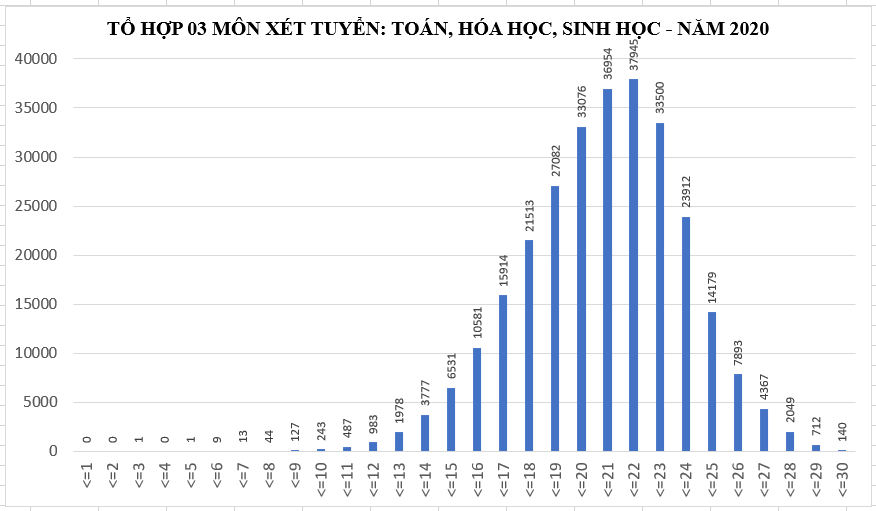
Trong NumPy, ta có thể tạo ra một mảng dựa trên phân phối chuẩn bằng hàm random.normal có cú pháp:

numpy.random.normal(loc=0.0, scale=1.0, size=None) # loc = mean, scale = standard deviation

Ví dụ:

m, sigma = 0, 0.1 # mean và standard deviation
s = np.random.normal(mu, sigma, size=5)
s

array([1.04652266, 1.01122791, 1.17575078, 0.92608879, 1.06772102])

numpy.random.randn

Đây cũng là một hàm sinh ra một mảng số tuân theo phân phối chuẩn, nhưng kết quả trả về là mảng có các phần tử phân bố theo phân phối chuẩn có mean = 0 và standard deviation = 1 (phân phối được chuẩn hoá). Hàm random.randn khá đơn giản, nó chỉ nhận duy nhất các tham số là một dãy số tương ứng với số chiều của mảng, chẳng hạn:

np.random.randn(3, 3)

array([[ 0.03777261, -0.13544849, -0.01002595],
       [ 1.67080819, -0.66437971, -0.60555494],
       [-0.65099088,  0.51256776,  0.26238882]])

Vì là phân phối được chuẩn hoá nên ta có thể sử dụng hàm này thay cho random.normal trên như sau:

sigma * np.random.randn(...) + m 

numpy.random.uniform

Hàm này sẽ sinh ra một mảng có giá trị phân phối đều (uniform distribution) trong một khoảng nhất định cho trước. Hàm có cú pháp như sau:

numpy.random.uniform(low=0.0, high=1.0, size=None)

Trong phân phối đều, các mẫu được phân bố đồng đều trong khoảng [low, high). Hàm mật độ xác suất của phân phối đều là:

Với b = high, a = low.

Đây là đồ thị của 1 phân phối đều:

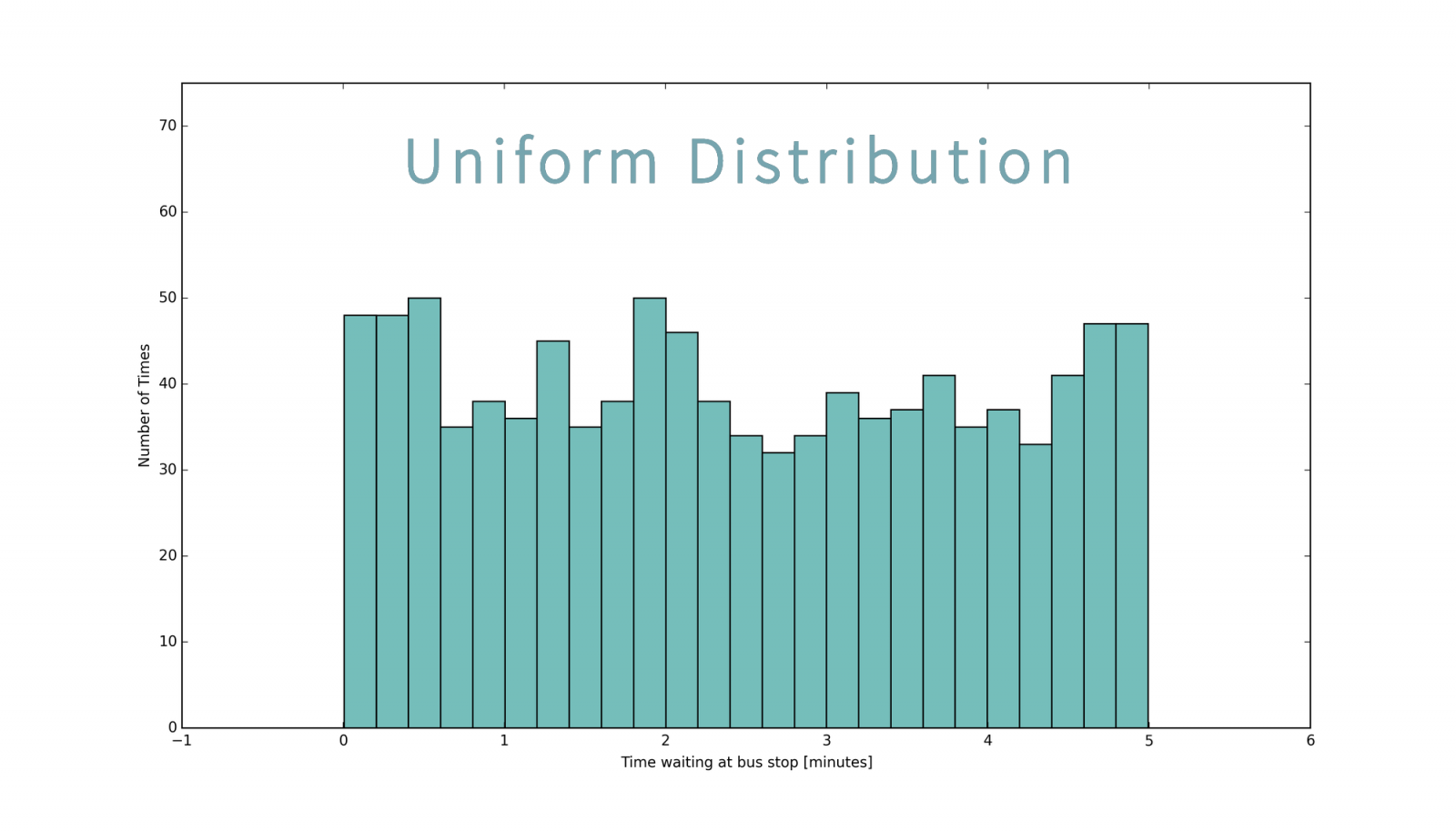
Để tạo một phân phối đều trong NumPy:

u = np.random.uniform(size=4)
print(u)

[0.95339335 0.00394827 0.51219226 0.81262096]

numpy.random.permutation

Hàm có cú pháp như sau:

numpy.random.permutation(x)

Mục đích của hàm chính là tạo nên một dãy hoán vị, chẳng hạn:

p = np.random.permutation(10)
print(p)

[0 7 5 2 3 9 6 4 8 1]

Ví dụ trên tạo ra một mảng có 10 phần tử bao gồm các số tự nhiên từ 0 đến 9 sắp xếp theo thứ tự ngẫu nhiên, mảng này chính là hoán vị của các số từ 0 đến 9.

3. Tổng kết

Vậy là ta đã kết thúc bài dài nhất trong chương NumPy, đây là một có một ít kiến thức về toán nên có thể sẽ có nhiều người hơi bối rối. Trong bài tiếp theo, ta sẽ tìm hiểu về Masks - một tính năng vô cùng hữu ích trong NumPy. Hẹn gặp bạn ở bài tiếp.