Đếm đối tượng trong các khu công nghiệp là một bài toán đã có từ lâu đời. Phương pháp đếm đối tượng hiệu quả không những giúp cho các nhà quản lý kiểm tra được chất lượng quy trình mà còn giải phóng lực lượng lao động.
Ngày nay, với sự phát triển rầm rộ của Machine Learning, người ta có thể nay lập tức cố gắng áp dụng mạng Neuron Network với những mô hình đồ sộ để giải quyết bài toán. Tuy thế, các phương pháp truyền thống vẫn chứng mình được tính hiệu quả của mình với độ chính xác cao và không yêu cầu cấu hình máy xử lý lớn
Ở bài này trong ta cùng tìm hiểu phương pháp được đề xuất vào tháng 2/2018, trong bài báo: An Image Processing based Object Counting Approach for Machine Vision Application với ứng dụng đếm số lượng trứng hay số lượng chai nước ngọt trong nhà máy
I. Phương pháp được đề xuất

1. Lấy ảnh chụp từ camera
2.Chuyển đổi thang màu sắc
Ảnh chụp từ camera khi được mã hóa thường được thẻ hiện dưới dạng RGB (Red, Green, Blue). Trong bài toán đếm số lượng trứng hay chai nước ngọt, màu sắc của vật thể không phải là đại lượng đáng quan tâm, nên ta chuyển qua hệ màu HSV (Hue – sắc thái, Saturation – độ bão hòa (độ đậm nhạt), Value – độ sáng tối).
3. Lấy ra độ bão hòa (đậm nhạt) của ảnh
Như vừa đề cập, sắc thái (màu sắc vật thể) không đáng quan tâm, và vì khay chứa đồ luôn đi qua và được chụp ở một điều kiện ánh sáng như nhau, nên độ sáng tối cũng không cần thiết. Ở bài toán này, các tác giả chỉ lấy giá trị độ bão hòa (độ đậm nhạt) của ảnh để tiếp tục phân tích.
4. Sử dụng Gaussian Filter
Gaussian Filter có tác dụng làm giảm nhiễu từ ảnh. Có thể do chất lượng camera hoặc bản thân vật thể, 2 pixels trên quả trứng hoàn toàn có thẻ có độ đậm nhạt rất khác biệt, điều này khiến cho việc xử lý ảnh trở lên phức tạp và nhiều nhiễu. Để giảm thiểu sự khác biệt này hay làm mượt bức ảnh, các tác giả đã áp dụng gaussian filter: giá trị pixels sẽ bằng các giá trị trung bình của các pixels gần nó, với hệ số cho mỗi pixel được dựa trên phần bố chuẩn (Normal Distribution). Vùng áp dụng gaussian filter càng lớn (sigma càng lớn), thì ảnh sẽ càng mờ và mượt như ví dụ dưới đây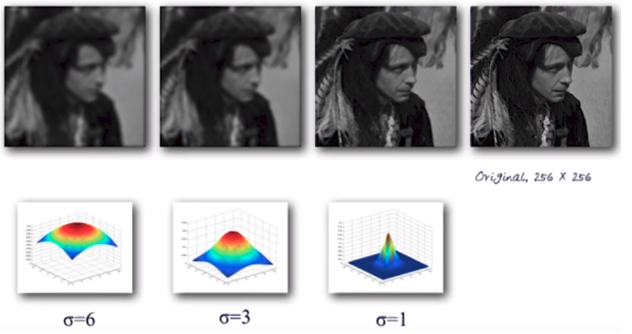
5. Sử dụng ngưỡng Otsu
Các giá trị độ đậm nhạt của mỗi pixel sẽ nằm trong khoảng từ 0 đến 255. Để nhìn rõ đường viền của các vật thể hơn, ta sẽ chọn một ngưỡng alphaα để với mỗi pixel có giá trị nhỏ hơn alphaα, ta gán pixel giá trị 0; pixcel có giá trị lớn hơn alphaα, ta gán pixel giá trị 255.
Từ giá trị pixel của toàn ảnh, ta biểu diễn toàn bộ các giá trị đó trên biểu đồ histogram (hình giữa), và ngưỡng Otsu được chọn thường là giá trị xấp xỉ điểm chính giữa của 2 đỉnh lớn nhất trong biểu đồ.

6. Phương pháp phát hiện đường viền Sobel
Sử dụng 2 bộ lọc Gx Mask và Gy Mask dưới đây để xác định được sự thay đổi độ lớn theo chiều dọc và chiều ngang của ảnh
Giá trị Gx, Gy được tính bằng tổng đại số của tích 9 giá trị pixel với 9 giá trị trong Gx Mask hoặc Gy Mask. Để ý kĩ, ta sẽ thấy giá trị Gx Mask từ trái qua phải tăng dần => khi thực hiện phép tính Gx, nếu giá trị pixel trên ảnh có sự tháy đổi lớn từ trái qua phải hay ngược lại, Gx sẽ rất lớn hoặc rất bé. Nếu giá trị 9 pixel không có sự thay đổi từ trái qua phái => Gx ~ 0.
Ta trượt Gx Mask và Gy Mask qua toàn bộ ảnh từ trái qua phải, từ trên xuống dưới, ta sẽ biết được tại một vị trí, liệu ảnh có sự chuyển dịch giá trị lớn không. G đại diện cho độ lớn của sự thay đổi (viền của ảnh).
Giá trị atan = Gx/Gy đại diện cho hướng của sự thay đổi (chiều đi của viền ảnh tại điểm đó). Sử dụng hướng atan và độ lớn G, ta có thể biểu diễn viền 1 cánh hoa cùng hướng sự thay đỏi tại mỗi pixel (màu sắc ứng với hướng sự thay đổi) như hình dưới đây. 
Ở ứng dụng nhận diện trứng hay chai nước ngọt, ta chỉ quan tâm đến viền => giá trị G (độ lớn của sự thay đổi)
7. Phương pháp biến đổi Hough
Phương pháp biến đổi Hough cho phép kết nối đường viền của vật thể. Để nhận diện trứng hay chai nước ngọt, biến đổi đường tròn Hough được sử dụng. Tuy thế, để dễ hiểu hơn về phương pháp này, ta cùng tìm hiểu biến đổi đường thẳng Hough, biến đổi đường tròn dựa trên lý thuyết tương tự.
Đường thẳng được đại diện bởi hàm số y = ax + b, với x, y là biến số là các trục tọa độ; a,b là tham số. Với biến đổi Hough, ta coi x, y là tham số và a, b là biến số: b = -xa + y. Giá trị x, y là giao của 2 đường thẳng trên hệ tọa độ mới
Ta lại có thể tiếp tục biểu diễn đường thẳng b = -xa + y dưới dạng acos hetaθ + bsin hetaθ = hoρ với đại lượng hetaθlà góc với trục a, còn hoρ là khoảng cách từ tâm tọa độ tới đường thẳng (Trong hình dưới đây, a, b đã được thay thế bởi x, y)
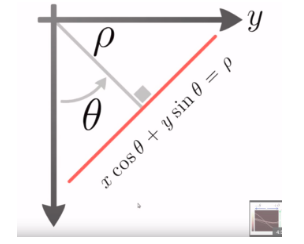
Với mỗi điểm trên ảnh, ta quay tất cả các đường thẳng (màu xanh) có thể để tìm các giá trị tương ứng hetaθ và hoρ. Mỗi một đường thẳng đi qua 1 điểm sẽ cho 1 cặp giá trị ( hetaθ, hoρ). Tất cả các đường thẳng đi qua 1 điểm sẽ cho 1 đường cong trên hệ tọa độ hetaθ và hoρ. Cặp giá trị ( hetaθ, hoρ) được đi qua càng nhiều (màu vàng), càng chứng tỏ tồn tại nhiều điểm trên hình ảnh gốc có chung 1 đường thẳng đi qua => liên kết cả điểm này, ta sẽ tìm được đường thẳng trên bức ảnh.
 Phương pháp phát hiện đường tròn Hough được dựa trên nguyên lý tương tự.
Phương pháp phát hiện đường tròn Hough được dựa trên nguyên lý tương tự.
II. Kết quả
Với việc đếm vật thể hình tròn, riêng biệt, không bị đè hay che khuất như trong điều kiện nhà máy, phương pháp này đạt kết quả tuyệt đối
| Thí nghiệm | Trứng | Chai nước ngọt |
|---|---|---|
| Toàn bộ quá trình |  |
 |
| Thí nghiệm khác |  |
 |
III. Ứng dụng mẫu
Áp dụng nhận diện hình tròn trong logo CV2 Mọi người có thể tham khảo đoạn code mẫu dưới đây:
Mọi người có thể tham khảo đoạn code mẫu dưới đây:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# Tách độ sáng tối (channel v) từ ảnh import cv2 import numpy as np from matplotlib import pyplot as plt img = cv2.imread('opencv.png') gray = cv2.cvtColor(img, cv2.COLOR_BGR2HSV) h, s, v = cv2.split(gray) plt.imshow(v, 'gray') plt.show() |
Với ảnh OpenCV2 logo như đầu vào, ta dùng độ sáng tối (channel v) thay cho độ đạm nhạt (channel s)
|
1 2 3 4 5 6 |
# Loại bỏ nhiễu blur = cv2.GaussianBlur(v,(3,3),0) plt.imshow(v, 'gray') plt.show() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# Áp dụng ngưỡng Otsu ret,th = cv2.threshold(blur,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU) plt.subplot(1,3,1), plt.imshow(blur, 'gray') plt.title('Gaussian filtered Image'), plt.xticks([]), plt.yticks([]) plt.subplot(1,3,2), plt.hist(blur.ravel(), 256) plt.title('Histogram'), plt.xticks([]), plt.yticks([]) plt.subplot(1,3,3),plt.imshow(th,'gray') plt.title('Otsu Thresholding'), plt.xticks([]), plt.yticks([]) plt.show() cv2.imwrite('otsuThesholding.jpg', th) |
|
1 2 3 4 5 6 7 8 9 10 |
# Sử dụng phát hiện đường viền Sobel sobel = cv2.Sobel(th,cv2.CV_8UC1,1,1,ksize=5) plt.subplot(1,1,1),plt.imshow(sobel,cmap = 'gray') plt.title('Sobel Edge detection'), plt.xticks([]), plt.yticks([]) plt.show() cv2.imwrite('sobel.jpg',sobel) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# Sử dụng biến đổi Hough để phát hiện hình tròn gray_img = cv2.imread('sobel.jpg', 0) cimg = cv2.cvtColor(sobel,cv2.COLOR_GRAY2BGR) circles = cv2.HoughCircles(gray_img,cv2.HOUGH_GRADIENT,1,20, param1=45,param2=32,minRadius=0,maxRadius=0) circles = np.uint16(np.around(circles)) for i in circles[0,:]: cv2.circle(cimg,(i[0],i[1]),i[2],(0,255,0),2) cv2.circle(cimg,(i[0],i[1]),2,(0,0,255),3) plt.subplot(122),plt.imshow(cimg) plt.title('Hough Transform'), plt.xticks([]), plt.yticks([]) plt.show() cv2.imwrite('houghCircle.jpg', cimg) |
IV. Kết luận
Bằng cách sử dụng một loạt các phương pháp biến đổi hình ảnh, cùng với xác định những ngưỡng bằng tay (ví dụ như tham số giới hạn bán kính của các đường tròn trong hàm cv2.HoughCircles), ta có thể đếm được số lượng vật thể một cách dễ dàng với những bài toán vật thể tách biệt, không đè lên nhau hay bị che khuất.
Lợi thế của phương pháp này là không yêu cầu cấu hình máy lớn và tốc độ tính toán xử lý rất nhanh, phù hợp với bài toán liên quan đến camera, khi các khung hình được đưa vào liên tục. Phương pháp này hoàn toàn có thể được ứng dụng đếm vật thể trong các khu công nghiệp.
Hy vọng các bạn có thể ứng dụng phương pháp này vào thực tế hoặc hiểu thêm về những hướng đi xử lý ảnh thông qua bài viết này.

