Dùng Python 3 tính xác suất thoát FA
Lời tựa Dạo này đọc Framgia Confession, thấy nhiều bạn đang FA, mong muốn được gởi tình cảm đến bạn này bạn kia…Chứng tỏ, mong muốn thoát khỏi độc thân của các Framgia-er khá là cao (haha). Mở bài hơi liên quan, hôm nay mình muốn giới thiệu cho các bạn một bài viết khá thú vị: Dùng thuật ...
Lời tựa Dạo này đọc Framgia Confession, thấy nhiều bạn đang FA, mong muốn được gởi tình cảm đến bạn này bạn kia…Chứng tỏ, mong muốn thoát khỏi độc thân của các Framgia-er khá là cao (haha). Mở bài hơi liên quan, hôm nay mình muốn giới thiệu cho các bạn một bài viết khá thú vị: Dùng thuật toán trong Python 3 để tính xác suất thoát FA một cách tối ưu nhất. Mời các bạn đọc bài và tự tính tỉ lệ cho bản thân nha. Have Fun!
Nội dung bài dịch Hiện nay, tại Nhật Bản, trong số những người dưới 50 tuổi thì: Cứ 4 nam thì có 1 người không kết hôn. Tỉ lệ này với nữ giới là 1/7. Xu hướng không kết hôn ở cả hai giới đều đang tiếp tục tăng lên (nguồn: báo Huftington). Nguyên nhân của tình trạng này thì có rất nhiều, nhưng có vẻ lý do thuộc hàng Top cho tỉ lệ kết hôn thấp, đó là “Không tìm thấy đối phương thích hợp”. Tuy nhiên, vấn đề đặt ra là: “Về tổng thể, đối phương thích hợp là đối phương như thế nào?” Các tiêu chí, điều kiện, yêu cầu với đối phương như: Thu nhập, ngoại hình, tính cách, nhà cửa….v.v với mỗi người sẽ có sự khác nhau. Dẫu biết trăm năm là hữu hạn, dù đã gặp được đối tượng có vẻ phù hợp… nhưng cũng không ít người có suy nghĩ “Biết đâu sau đó lại tìm được đối tượng tốt hơn thì sao?” Cứ chần chừ như vậy nên nhiều khi các bạn đã tự đánh mất cơ hội của chính mình (khoc). Tôi xin tóm lược phương pháp tối ưu để tính xác suất tìm được người vợ tiềm năng của các chàng trong bài toán dưới đây: Giả sử có 1 anh A – đang kiếm Gấu để sau này cưới vợ.
- Anh A có thể gặp được N cô gái – tổng số những ứng viên tiềm năng mà anh A có thể gặp gỡ hẹn hò.
- ứng viên tiềm năng sẽ xuất hiện lần lượt từng người một.
- Mỗi ứng viên sẽ mang những điểm số khác nhau (do anh A tự chấm)
- Anh A muốn kết hôn với cô nào có số điểm cao nhất (dĩ nhiên:v)
- Sau khi anh A nói Yes (đồng ý kết hôn) với một cô gái, thì anh A sẽ không thể tiếp tục gặp gỡ, hẹn hò các cô gái còn lại trong N cô gái được nữa.
- Với các ứng viên mà anh A said No (không cưới) thì anh A có thể tiếp tục đi gặp gỡ hẹn hò các cô nàng tiềm năng khác và không thể hẹn hò lại người cũ. Bài toán trên được gọi là Secretary Problem. Trong đó, có chứa option số học tối ưu nhất. Đó là:
- 37% số người đầu tiên sẽ bị nói Không, dù ứng viên có bao nhiêu điểm đi chăng nữa (có vẻ mối tình đầu thường Fail là vậy=))
- Những người sau đó: tính tới thời điểm hiện tại, Ai là người có số điểm cao nhất thì sẽ chọn người đó. Thật đơn giản các bạn ạ. Tỉ lệ 37% thực tế là từ phép tính sít sao 1/e. Theo option này, thì có vẻ xác suất anh A có thể kết hôn với người có điểm cao sẽ tăng lên không phụ thuộc vào số lượng ứng viên N. Tuy nhiên, khi nghe ý kiến này, chắc hẳn các bạn sẽ bán tín bán nghi “Có gì đó sai sai. Có thật không vậy?” Tôi hiểu là sẽ phải đặt một giá trị ngưỡng ở đâu đó, thường thì mọi người sẽ không đặt số lẻ 37% mà sẽ đặt con số là 50%, hoặc nếu phải chờ lâu thêm một chút nữa sẽ là 80% Lần này, tôi sẽ sử dụng một Simulation đơn giản để kiểm chứng option này. Thực hiện option. Sử dụng Python3 để tính toán. Cần phải import các thư viện sau:
# import libraries import random import numpy as np import matplotlib.pyplot as plt import seaborn as sns
Hàm số chính (Main funtion) sẽ là: Input số lượng các ứng viên, và số lượng người mà A có thể gặp gỡ hẹn hò đến khi A lập ra giá trị ngưỡng rồi chọn ra đối tượng có điểm số cao hơn giá trị ngưỡng ban đầu. Sau đó Output ra rank và Score của partner. Điểm của các ứng viên sẽ được lấy từ việc điều chỉnh random từ 0 đến 100.
# function to find a partner based on a given decision-time
def getmeplease(rest, dt, fig):
## INPUT: rest ... integer representing the number of the fixed future encounters
# dt ... integer representing the decision time to set the threshold
# fig ... 1 if you want to plot the data
# ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
# score ranging from 0 to 100
scoremax = 100
#random.seed(1220)
# sequence of scores
distribution = random.sample(range(scoremax), k=rest)
# visualize distribution
if fig==1:
# visualize distribution of score
plt.close('all')
plt.bar(range(1,rest+1), distribution, awidth=1)
plt.xlabel('sequence')
plt.ylabel('score')
plt.xlim((0.5,rest+0.5))
plt.ylim((0,scoremax))
plt.xticks(range(1, rest+1))
# remember the highest score among the 100 x dt %
if dt > 0:
threshold = max(distribution[:dt])
else:
threshold = 0
# pick up the first one whose score exceeds the threshold
partner_id = 1
partner_score = distribution[0]
t = dt
for t in range(dt+1, rest):
if partner_score < threshold:
partner_score = distribution[t]
else:
partner_id = t
break
else:
partner_score = distribution[-1]
partner_id = rest
# get the actual ranking of the partner
array = np.array(distribution)
temp = array.argsort()
ranks = np.empty(len(array), int)
ranks[temp] = np.arange(len(array))
partner_rank = rest - ranks[partner_id-1]
# visualize all
if fig==1:
plt.plot([decisiontime+0.5,decisiontime+0.5],[0,scoremax],'--k')
plt.bar(partner_id,partner_score, color='g', awidth=1)
return [partner_id, partner_score, partner_rank]
Ví dụ: Số lượng ứng viên là 10 người. Số lượng các cô gái mà anh A gặp khi tới điểm ngưỡng là sấp sỉ 37% - tức là 4 cô. Hàm số này getmeplease(10,4,1 sẽ được biểu diễn như trong biểu đồ dưới đây.
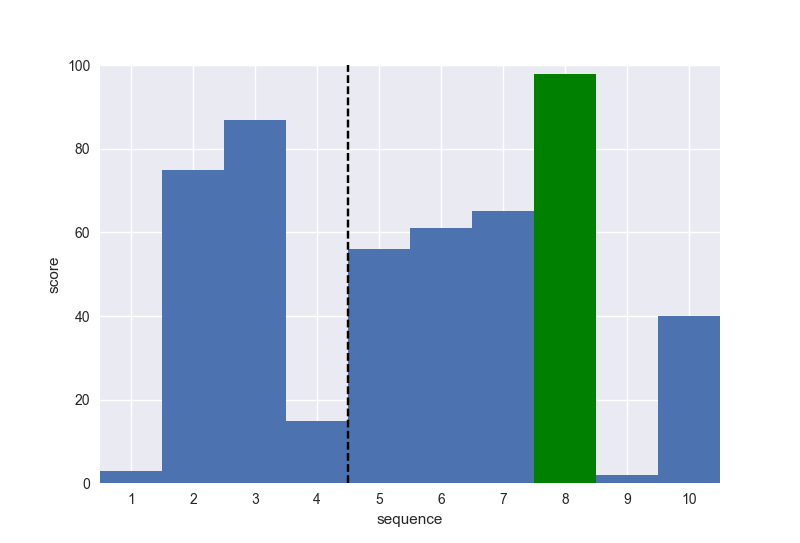
Trong 10 người, anh A đã có thể kết hôn với người có số điểm cao nhất – người sẽ xuất hiện ở lần thứ 8 (sugoi)
Simulation
Tôi tiếp tục thực hiện phép tính trên với 4 pattern: Số người có thể gặp gỡ được N là 5, 10, 20, 100. Tương tự như vậy, tôi dùng 4 pattern cho Số lượng các cô gái gặp được cho đến khi lập được giá trị ngưỡng, thay đổi từ 10%, 37%, 50%, 80% và so sánh các kết quả. Với hàm số dưới đây, tôi đã cho chạy Simulation 10.000 lần với các option ("optimal": 37%、"early": 10%、"late": 80%、"half": 50%) và đã lập được Rank, Histogram của từng ứng viên được lựa chọn, rồi request giá trị trung tâm
# parameters
repeat = 10000
rest = [5,10,20,100]
opt_dt = [int(round(x/np.exp(1))) for x in rest]
tooearly_dt = [int(round(x*0.1)) for x in rest]
toolate_dt = [int(round(x*0.8)) for x in rest]
half_dt = [int(round(x*0.5)) for x in rest]
# initialization
opt_rank = np.zeros(repeat*len(rest))
early_rank = np.zeros(repeat*len(rest))
late_rank = np.zeros(repeat*len(rest))
half_rank = np.zeros(repeat*len(rest))
opt_score = np.zeros(repeat*len(rest))
early_score = np.zeros(repeat*len(rest))
late_score = np.zeros(repeat*len(rest))
half_score = np.zeros(repeat*len(rest))
# loop to find the actual rank and score of a partner
k = 0
for r in range(len(rest)):
for i in range(repeat):
# optimal model
partner_opt = getmeplease(rest[r], opt_dt[r], 0)
opt_score[k] = partner_opt[1]
opt_rank[k] = partner_opt[2]
# too-early model
partner_early = getmeplease(rest[r], tooearly_dt[r], 0)
early_score[k] = partner_early[1]
early_rank[k] = partner_early[2]
# too-late model
partner_late = getmeplease(rest[r], toolate_dt[r], 0)
late_score[k] = partner_late[1]
late_rank[k] = partner_late[2]
# half-time model
partner_half = getmeplease(rest[r], half_dt[r], 0)
half_score[k] = partner_half[1]
half_rank[k] = partner_half[2]
k += 1
# visualize distributions of ranks of chosen partners
plt.close('all')
begin = 0
for i in range(len(rest)):
plt.figure(i+1)
plt.subplot(2,2,1)
plt.hist(opt_rank[begin:begin+repeat],color='blue')
med = np.median(opt_rank[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('optimal: %i' %int(med))
plt.subplot(2,2,2)
plt.hist(early_rank[begin:begin+repeat],color='blue')
med = np.median(early_rank[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('early: %i' %int(med))
plt.subplot(2,2,3)
plt.hist(late_rank[begin:begin+repeat],color='blue')
med = np.median(late_rank[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('late: %i' %int(med))
plt.subplot(2,2,4)
plt.hist(half_rank[begin:begin+repeat],color='blue')
med = np.median(half_rank[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('half: %i' %int(med))
fig = plt.gcf()
fig.canvas.set_window_title('rest' + ' ' + str(rest[i]))
begin += repeat
plt.savefig(figpath + 'rank_' + str(rest[i]))
begin = 0
for i in range(len(rest)):
plt.figure(i+10)
plt.subplot(2,2,1)
plt.hist(opt_score[begin:begin+repeat],color='green')
med = np.median(opt_score[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('optimal: %i' %int(med))
plt.subplot(2,2,2)
plt.hist(early_score[begin:begin+repeat],color='green')
med = np.median(early_score[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('early: %i' %int(med))
plt.subplot(2,2,3)
plt.hist(late_score[begin:begin+repeat],color='green')
med = np.median(late_score[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('late: %i' %int(med))
plt.subplot(2,2,4)
plt.hist(half_score[begin:begin+repeat],color='green')
med = np.median(half_score[begin:begin+repeat])
plt.plot([med, med],[0, repeat*0.8],'-r')
plt.title('half: %i' %int(med))
fig = plt.gcf()
fig.canvas.set_window_title('rest' + ' ' + str(rest[i]))
begin += repeat
plt.savefig(figpath + 'score_' + str(rest[i]))
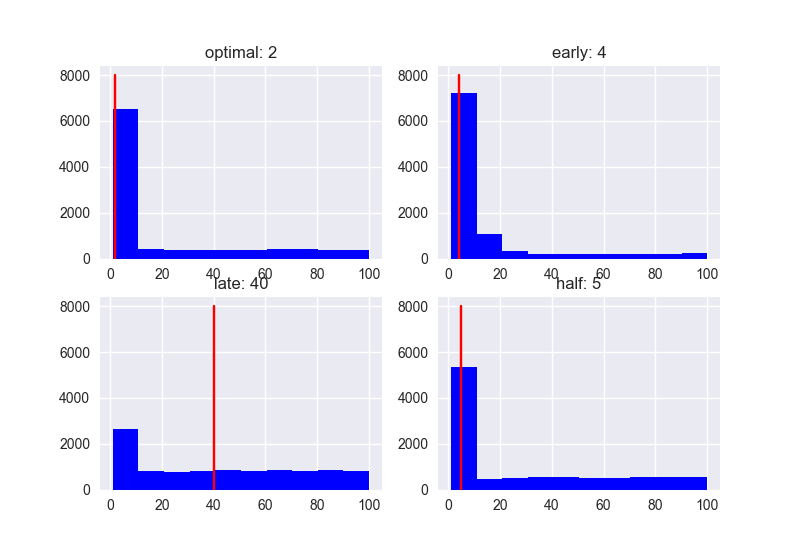
Nếu N = 20 Nếu anh A gặp 20 người, thì Score và Rank của các ứng viên sẽ được phân bổ như ảnh sau:
Rank
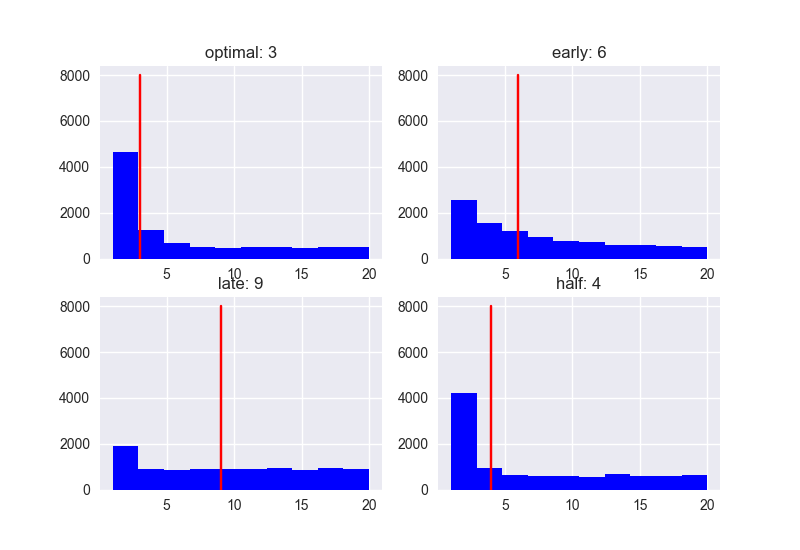
Nếu sử dụng option Optimal(37%) thì giá trị trung bình của rank sẽ là 3. Theo tiền đề ở đầu bài “Nói Không với 37% đầu tiên. Sau đó sẽ nói CÓ với người có điểm số cao nhất” thì trong những ứng viên có điểm số lớn nhất, anh A có thể kết hôn với 1 trong 3 người đứng đầu. Ngoài ra, giá trị trung bình của Early (10%) và Half (50%) lần lượt là 6 và 4 => Nếu chọn thì sẽ không tốt lắm. Với Late (80%), giá trị trung bình là 9 => tỉ lệ thất bại lại càng cao hơn. Thế còn điểm số (Score) thì sao?
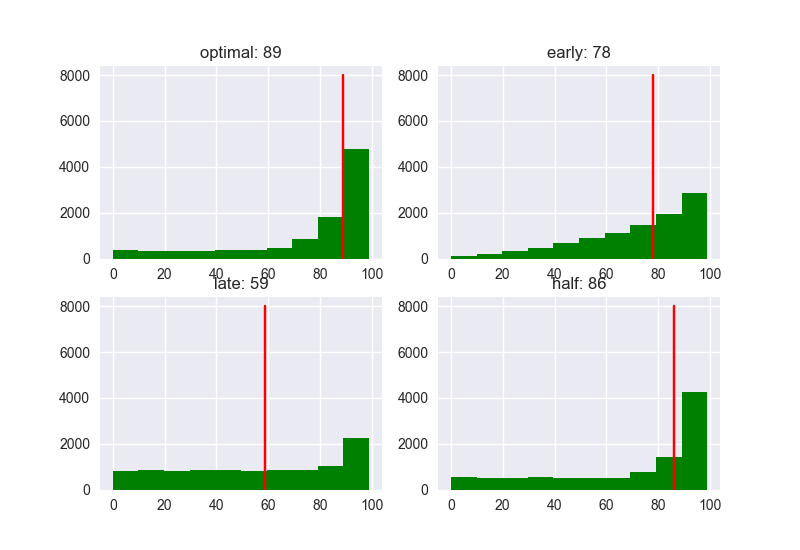
Nếu dùng option Optimal (37%): thì giá trị trung bình của Score là 89. Với các option khác: Early (10%)が78、Late (80%) là 59, Half (80%) là 86 nên khi quyết định giá trị ngưỡng 1/e thì performance khá cao. Anh A chọn được vợ dễ dàng hơn. ở đây chiến lược tối ưu nhất không phải là đưa ra lời giải tối ưu nhất, mà là việc : Làm sao để tăng tính khả thi để đến gần với lời giải hay nhất. Tôi sẽ xét các trường hợp: số lượng ứng viên lần lượt là : 5 người, 10 người, 100 người. N = 5 Rank
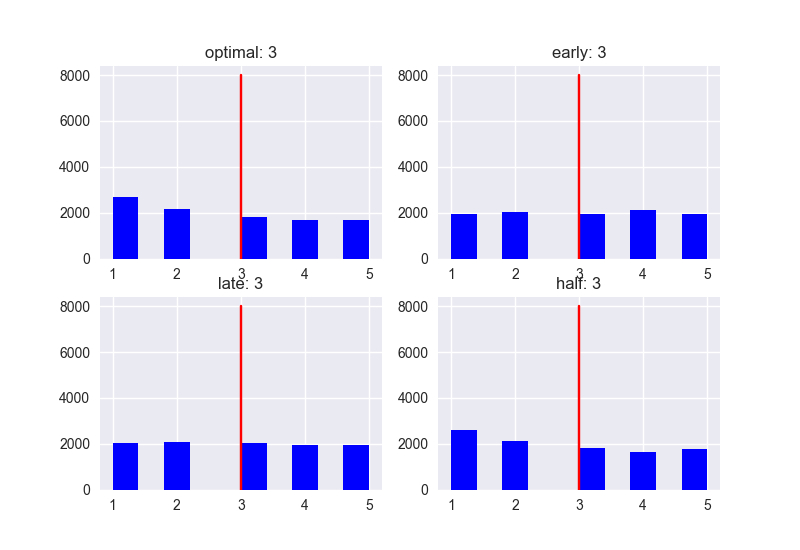
Score
N = 10
Rank
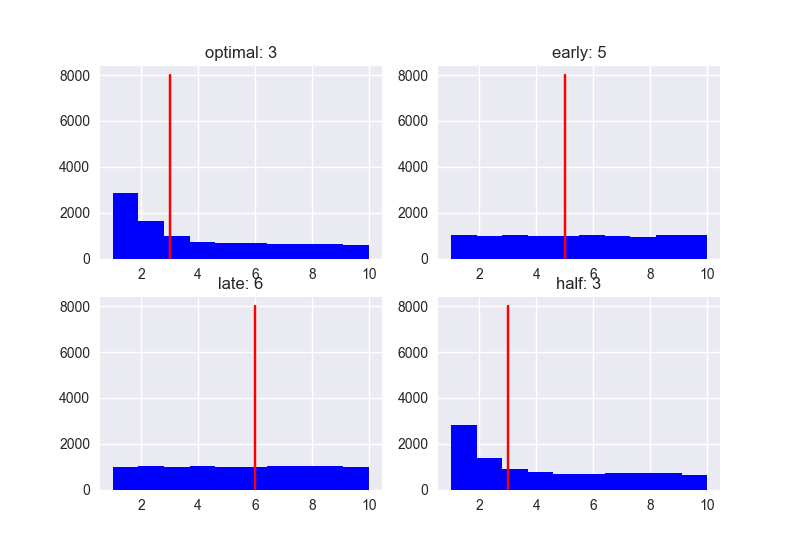
Score
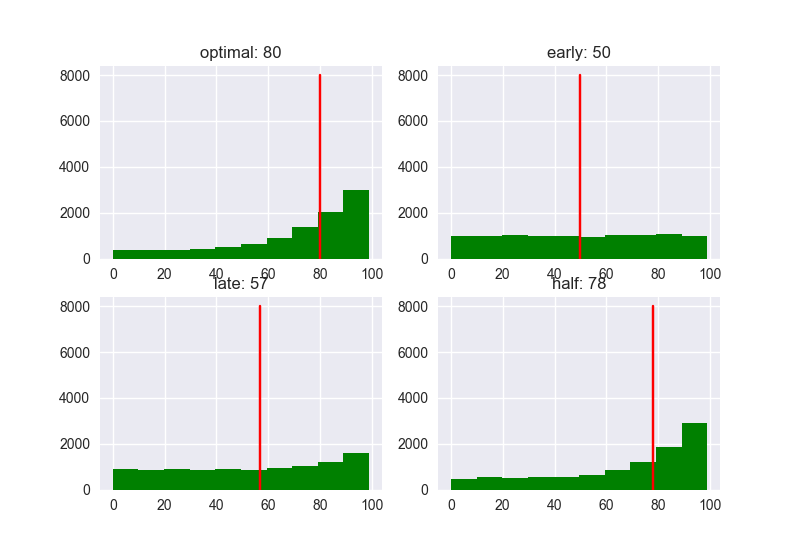
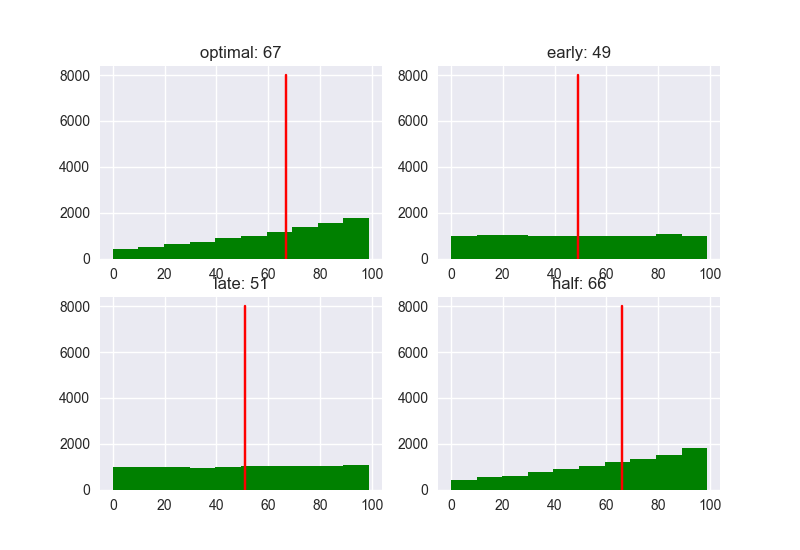
N = 100
Rank
Score
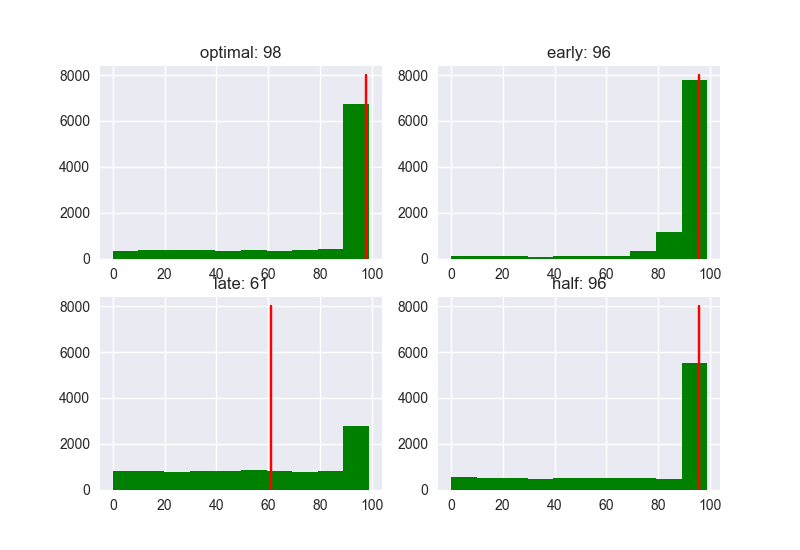
Dựa theo các biểu đồ trên, có thể thấy xu hướng: Khi số lượng ứng viên càng tăng lên thì Performance, đặc biệt là với nhóm late càng tệ. Nếu số lượng ứng viên ít thì Performance có khác nhau đôi chút, nhưng điểm Score có xu hướng thấp dần. ở bất kì trường hợp nào: Người gặp đầu tiên sau khi đã trừ 37% sẽ là người có khả năng có Rank và Score cao nhất => là ứng viên tiềm năng nhất cho A.
Kết luận
• Càng có nhiều ứng viên, thì càng có khuynh hướng phân vân đâu là người tốt hơn. • Tuy nhiên, nếu cứ phân vân “ Tôi muốn suy nghĩ kỹ hơn…” thì bạn không chỉ làm mất cơ hội, mà người bạn chọn sau cùng cũng có điểm số thấp. • Sớm quá cũng không tốt. • Quyết định số lượng cô gái từ giờ mình sẽ gặp. Quyết định giá trị ngưỡng 1/e và sau đó chọn người đầu tiên có điểm vượt quá giá trị ngưỡng. Đó là người thích hợp nhất cho bạn.
Chú ý
• Đời không như là mơ, Có những trường hợp: Mình say Yes nhưng đối phương say No. • Những anh chàng không có đối tượng nào (Những người mà ngày nghỉ cũng ở nhà ngồi Code) • Dù chọn được chiến lược tối ưu nhưng cũng không có nghĩa là sẽ lấy được kết quả tối ưu nhất Nhưng dù sao thì các bạn hãy cố gắng nhé. Cơ hội ít còn hơn không!=))
Link bài gốc: http://qiita.com/katsu1110/items/248097d7aea58e643749?utm_source=Qiita Sưu tầm và dịch bài: Thanh Thảo
