Mô hình hồi quy ứng dụng trong bài toán dự đoán giá bất động sản - Machine Learning (phần 2)

Xin chào tất cả các bạn. Ngày hôm nay chúng ta sẽ cùng nhau quay trở lại với serial về bài toán dự đoán trong học máy. Phần trước đó, các bạn có thể tham khảo ở đây. Trong bài này mình sẽ trình bày với các bạn về mô hình hồi quy và một ứng dụng cụ thể mình đã áp dụng trong một Project thực hiện trong quá trình Training tại Framgia Vietnam đó là ứng dụng định giá bất động sản. OK chúng ta bắt đầu nhé.

Vấn đề

• Đã có một tập dữ liệu gồm các thuộc tính của bất động sản và giá của chúng
• Các thuộc tính như: số phòng ngủ, số phòng tắm, vị trí địa lý, năm xây dựng...và giá bán
• Giờ muốn tìm một công thức nào đó để từ một bất động sản bất kì, cho biết một vài thông tin như số phòng ngủ, vị trí địa lý... có thể tính toán ra được giá bán

Hướng giải quyết

OK, nếu các bạn đã theo dõi bài trước của mình thì sẽ thấy được qua ví dụ hoang tưởng là việc tính xổ số, chúng ta có thể ứng dụng chính mô hình đó cho tính giá bất động sản. Nói sơ qua một chút về lý thuyết cho các bạn hiểu về mô hình hồi quy nhé. Bản chất của hồi quy chính là tìm ra mối quan hệ nào đó giữa biến phụ thuộc (dependence) Y (ví dụ như kết quả xổ số hay giá nhà) và một hay nhiều biến độc lập X (independence) ví dụ như các thuộc tính của ngôi nhà chẳng hạn. Chúng ta cùng tìm hiểu một mô hình hồi quy đơn giản nhất đó chính là Hồi quy tuyến tính nhé.

Mô hình hồi quy tuyến tính

Đối với mô hình hồi quy tuyến tính, mô hình hóa sử dụng là dạng bậc nhất. Có nghĩa là chúng ta cần tính toán các hệ số Wi trong một biểu thức bậc nhất như sau:

Y = W0 + W1.X1 + W2.X2 + ... + Wn.Xn

Tức là trên đồ thị chúng ta đi tìm một đường thẳng (nếu trường hợp có 1 biến độc lập) hoặc một siêu phẳng (với trường hợp nhiều biến độc lập) đi qua tập hợp các điểm trong không gian thuộc tính mà thể hiện gần đúng nhất sự phân bố của tập dữ liệu. Trên phương diện tính toán, chúng ta đi tìm các hệ số Wi như trên sao cho lỗi hồi quy đạt được là nhỏ nhất. Lại nói về lỗi hồi quy người ta thường sử dụng Phương pháp bình phương nhỏ nhất (least square). Các bạn có thể tham khảo thêm ở đây

Ứng dụng vào bài toán dự đoán giá bất động sản

Cái đầu tiên muốn nói gì thì nói chúng ta cần phải có một tập dữ liệu.Tập dữ liệu trong bài viết này các bạn có thể tìm thấy ở đây. File CSV này chứa thông tin về các bất động sản như số phòng ngủ, số phòng tắm, năm xây dựng... và giá bán tương ứng của nó. Chúng ta sẽ áp dụng lý thuyết về mô hình hồi quy để từ tập dữ liệu này, xây dựng một hàm sử dụng để định giá cho một bất động sản bất kì trong tương lai. OK chúng ta bắt đầu thôi.

Đọc dữ liệu từ file CSV

Trước tiên các bạn cần cài đặt Python và các thư viện cần thiết. Như phiên bản hiện tại mình đang sử dụng là Python 2.7 và Scikit-learn 0.18.1. Sau khi cài đặt các môi trường cần thiết. Chúng ta hãy viết một hàm để load dữ liệu từ file CSV bên trên như sau:

import os
import pandas as pd

def getData():
    # Get home data from CSV file
    dataFile = None
    if os.path.exists('home_data.csv'):
        print("-- home_data.csv found locally")
        dataFile = pd.read_csv('home_data.csv', skipfooter=1)

    return dataFile

Hàm trên sử dụng thư viện Pandas để load dữ liệu từ file CSV vào dưới dạng DataFrame

Lựa chọn thuộc tính và phân chia tập dữ liệu mẫu

Tư tưởng của chúng ta là sẽ phân chia tập dữ liệu mẫu thành hai tập con là tập dữ liệu huấn luyện và tập dữ liệu kiểm tra. Việc này sử dụng tư tưởng của kiểm tra chéo (cross validation). Ngoài ra, trong tập dữ liệu mẫu có rất nhiều thuộc tính có ý nghĩa và có thể khai thác thêm, ví dụ như từ kinh độ và vĩ độ chúng ta có thể tìm thêm các thuộc tính như khoảng cách trung tâm thành phố, số bệnh viện lân cận... Tuy nhiên trong bài viết này để cho đơn giản, mình lựa chọn một cách chủ quan một số thuộc tính mà mình cho rằng có thể có ảnh hưởng đến giá của bất động sản như số phòng ngủ, số phòng tắm, năm xây dựng và diện tích... Tất nhiên rằng, lựa chọn thuộc tính là một bài toán khác trong học máy, các bạn có thể tham khảo ở đây nhưng trong phạm vi bài viết này chúng ta chưa bàn đến nó.

data = getData()
    if data is not None:
        # Selection few attributes
        attributes = list(
            [
                'num_bed',
                'year_built',
                'num_room',
                'num_bath',
                'living_area',
            ]
        )
        # Vector price of house
        Y = data['askprice']
        # Vector attributes of house
        X = data[attributes]
        # Split data to training test and testing test
        X_train, X_test, Y_train, Y_test = train_test_split(np.array(X), np.array(Y), test_size=0.2)

Đoạn code bên trên phân chia tập dữ liệu thành 5 phần tương ứng 80% cho training và 20% cho testing. Việc cần làm tiếp theo là viết một hàm chạy Phương pháp hồi quy tuyến tính.

Áp dụng mô hình hồi quy tuyến tính

Về cơ bản, việc huấn luyện theo mô hình tuyến tính bản chất là đi tìm các giá trị m và b sao cho cực tiểu hóa hàm lỗi sau:

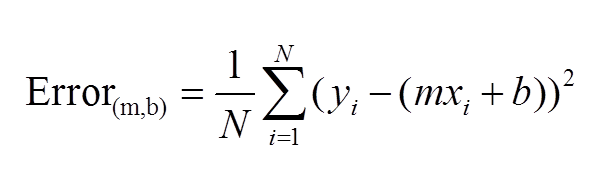
Chúng ta sử dụng gói thư viện Scikit-learn của Python để làm việc này rất đơn giản như sau:

def linearRegressionModel(X_train, Y_train, X_test, Y_test):
    linear = linear_model.LinearRegression()
    # Training process
    linear.fit(X_train, Y_train)
    # Evaluating the model
    score_trained = linear.score(X_test, Y_test)

    return score_trained

Hàm trên chạy mô hình hồi quy tuyến tính trên tập dữ liệu huấn luyện gồm X_train đại diện cho tập các thuộc tính của bất động sản và Y_train đại diện cho giá của nhà. Hàm trả về một giá trị đánh giá điểm của mô hình khi chạy trên tập kiểm tra. Về cơ bản, chúng ta có thể sử dụng điểm này để so sánh giữa các phương pháp hồi quy khác sẽ trình bày ở phần tiếp theo. Có nghĩa là điểm càng tiến gần đến 1 thì mô hình của chúng ta càng tốt.

Áp dụng mô hình hồi quy LASSO dạng chuẩn L1

Các dạng chuẩn (Regularization) thường được đưa vào các mô hình để nhằm giảm thiểu hiện tượng over-fitting. Nói về overfitting là cả một câu chuyện dài và mình hứa sẽ có dịp kể cho các bạn nghe về câu chuyện đó trên Viblo này. Chúng ta có thể hiểu nôm na như sau, một mô hình của chúng ta lựa chọn đang cố gắng giảm thiểu tối đa lỗi trên tập dữ liệu huấn luyện nhưng nó lại làm cho lỗi trên tập dữ liệu kiểm tra tăng lên. Và LASSO ra đời để hạn chế điều đó. Nó bổ sung thêm vào hàm lỗi của mô hình tuyến tính một đại lượng phạt lỗi lamda. Từ đó mô hình của chúng ta sẽ tìm các tham số phù hợp sao cho cực tiểu hóa hàm lỗi như sau:

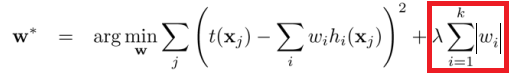
Chúng ta sẽ viết một hàm tính toán điểm của phương pháp LASSO như sau:

def lassoRegressionModel(X_train, Y_train, X_test, Y_test):
    lasso_linear = linear_model.Lasso(alpha=1.0)
    # Training process
    lasso_linear.fit(X_train, Y_train)
    # Evaluating the model
    score_trained = lasso_linear.score(X_test, Y_test)

Đánh giá hai mô hình hồi quy vừa áp dụng

Trong hàm main chúng ta chạy và so sánh hai hàm như sau:

if __name__ == "__main__":
    data = getData()
    if data is not None:
        # Selection few attributes
        attributes = list(
            [
                'num_bed',
                'year_built',
                'num_room',
                'num_bath',
                'living_area',
            ]
        )
        # Vector price of house
        Y = data['askprice']
        # print np.array(Y)
        # Vector attributes of house
        X = data[attributes]
        # Split data to training test and testing test
        X_train, X_test, Y_train, Y_test = train_test_split(np.array(X), np.array(Y), test_size=0.2)
        # Linear Regression Model
        linearScore = linearRegressionModel(X_train, Y_train, X_test, Y_test)
        print 'Linear Score = ' , linearScore
        # LASSO Regression Model
        lassoScore = lassoRegressionModel(X_train, Y_train, X_test, Y_test)
        print 'Lasso Score = ', lassoScore

Kết quả chạy như sau:

Connected to pydev debugger (build 162.1967.10)
-- home_data.csv found locally
Linear Score =  0.479529725484
Lasso Score =  0.479530220957
Process finished with exit code 0

Nếu dữ liệu và số lượng thuộc tính đủ lớn, ta có thể quan sát rõ tốc độ hội tụ của phương pháp Lasso nhanh hơn phương pháp hồi quy tuyến tính, nhờ vào cơ chế tính đạo hàm cho từng thuộc tính thay vì tính đạo hàm cùng lúc cho các thuộc tính. Cuối cùng, việc lựa chọn mô hình được dựa vào chỉ số đánh giá mô hình. Mô hình càng tốt thì model score càng gần đến 1.0.

Kết luận

Hồi quy là một phương pháp đơn giản và dễ áp dụng trong thực tế. Thực ra bài toán này còn có thể cải thiện hơn được nữa nhờ vào việc xấp xỉ căn bậc hai cho mô hình hay còn gọi là kĩ thuật nâng bậc cho mô hình tuyến tính mình sẽ tiếp tục trình bày trong các bài tiếp theo. Chúc các bạn cuối tuần vui vẻ. Xin chào tạm biệt và hẹn gặp lại.

Code và dữ liệu của bài viết

Các bạn cần tham khảo code áp dụng trong bài viết này và dữ liệu thì bơi vào đây

Tham khảo

Sklearn Regression

Coordinate descent

Gradient Descent