Neural Network Fundamental 4: Gradient descent, back propagation
Giả sử ta muốn minimize J(w1,w2,...)J(w_1, w_2, ...) J ( w 1 , w 2 , . . . ) . Nếu đây là 1 hàm sỗ phức tạp thì việc tìm 1 công thức tính w1,w2,...w_1, w_2, ... w 1 , w 2 ...
Giả sử ta muốn minimize J(w1,w2,...)J(w_1, w_2, ...)J(w1,w2,...). Nếu đây là 1 hàm sỗ phức tạp thì việc tìm 1 công thức tính w1,w2,...w_1, w_2, ...w1,w2,... cho J min là không dễ dàng. Gradient descent là thuật toán bắt đầu từ 1 giá trị nào đó của w1,w2,...w_1, w_2, ...w1,w2,... rồi đi từ từ từng bước một, mỗi bước lại update lại các parameter này và cuối cùng sẽ một giá trị mà J min.
Câu hỏi đặt ra là với mỗi bước sẽ đi như nào. Để đơn giản, xét ví dụ JJJ là hàm số 1 biến số J(w)J(w)J(w)
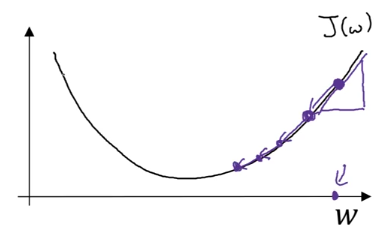 Từ giá trị www ban đầu (chấm bên phải ngoài cùng) ở mỗi bước ta update www theo rule sau
Repeat {
w:=w−αd(J(w))dww := w - alphadfrac{d(J(w))}{dw}w:=w−αdwd(J(w))
}
Trong đó αalphaα là learning rate quyết định ta bước mỗi bước ngắn hay dài
d(J(w))dwdfrac{d(J(w))}{dw}dwd(J(w)) > 0 tức J tăng lên khi ta tăng w lên 1 khoảng rất nhỏ nên ta trừ www đi 1 số dương là αd(J(w))dwalphadfrac{d(J(w))}{dw}αdwd(J(w))
Từ giá trị www ban đầu (chấm bên phải ngoài cùng) ở mỗi bước ta update www theo rule sau
Repeat {
w:=w−αd(J(w))dww := w - alphadfrac{d(J(w))}{dw}w:=w−αdwd(J(w))
}
Trong đó αalphaα là learning rate quyết định ta bước mỗi bước ngắn hay dài
d(J(w))dwdfrac{d(J(w))}{dw}dwd(J(w)) > 0 tức J tăng lên khi ta tăng w lên 1 khoảng rất nhỏ nên ta trừ www đi 1 số dương là αd(J(w))dwalphadfrac{d(J(w))}{dw}αdwd(J(w))
d(J(w))dwdfrac{d(J(w))}{dw}dwd(J(w)) < 0 tức J tăng lên khi ta giảm w lên 1 khoảng rất nhỏ nên ta trừ www đi 1 số âm là αd(J(w))dwalphadfrac{d(J(w))}{dw}αdwd(J(w)) nghĩa là cộng thêm αd(J(w))dwalphadfrac{d(J(w))}{dw}αdwd(J(w)) Khi w gần tới giá trị J min thì độ dốc của hàm số nhỏ đi do đó các bước ta đi cũng nhỏ đi
Chúng ta hãy nhắc lại một chút ở bài trước, loss function cho tất cả m training example
J(W[1],b[1],...)=1m∑i=1mL(y^i,yi)J(W^{[1]}, b^{[1]}, ...) = frac{1}{m}displaystylesum_{i=1}^mL(hat y^{i}, y^{i})J(W[1],b[1],...)=m1i=1∑mL(y^i,yi)
Trong đó L(y^i,yi)L(hat y^{i}, y^{i})L(y^i,yi) là loss function tính cho training example i
Mục tiêu của chúng ta là tìm giá trị của W[1],b[1],...W^{[1]}, b^{[1]}, ...W[1],b[1],... sao cho J nhỏ nhất.
Thực hiện gradient descent mỗi bước ta tính partial derivative (đạo hàm riêng) của từng layer: W[l]W^{[l]}W[l], b[l]b^{[l]}b[l]
Repeat {
dW[1]=dJdW[1]dW^{[1]} = dfrac{dJ}{dW^{[1]}}dW[1]=dW[1]dJ, db[1]=dJdb[1]db^{[1]} = dfrac{dJ}{db^{[1]}}db[1]=db[1]dJ, ...
W[1]=W[1]−α dW[1]W^{[1]} = W^{[1]} - alpha,dW^{[1]} W[1]=W[1]−αdW[1]
b[1]=b[1]−α db[1]b^{[1]} = b^{[1]} - alpha,db^{[1]} b[1]=b[1]−αdb[1]
...
}
dW[1]dW^{[1]}dW[1] là ma trận có cùng chiều với W[1]W^{[1]}W[1] chứa đạo hàm riêng của từng phần tử trong WWW với JJJ
db[1]db^{[1]}db[1] là vector có cùng chiều với b[1]b^{[1]}b[1] chứa đạo hàm riêng của từng phần tử trong b[1]b^{[1]}b[1] với JJJ
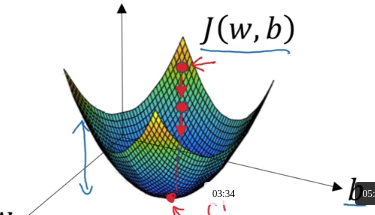
Nếu tập hợp tất cả các parameter W[1],b[1],...W^{[1]}, b^{[1]}, ...W[1],b[1],... thành 1 vector D. Kiến thức trong giải tich nhiều biến số cho ta biết là vector gradient của D cho ta hướng mà hàm số tăng nhanh nhất. Nên nếu ta muốn chiều mà hàm số đang giảm, ta update các parameter đó bằng cách trừ đi learning rate × imes× partial derivative

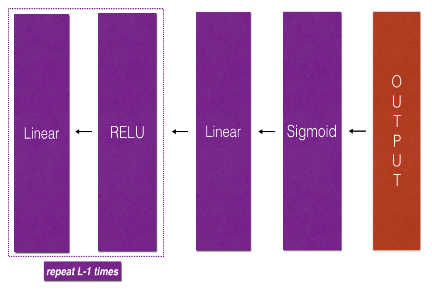
Ta nhắc lại một chút, forward propagation thực hiện việc tính toán input layer →
ightarrow→ hidden layer →
ightarrow→ nếu như đã biết trước W[l],b[l],...W^{[l]}, b^{[l]}, ...W[l],b[l],... của mỗi layer
for l = 1..L
z[l]=W[l]a[l−1]+b[l]z^{[l]} = W^{[l]}a^{[l - 1]} + b^{[l]}z[l]=W[l]a[l−1]+b[l]
a[l]=g(z[l])a^{[l]} = g(z^{[l]})a[l]=g(z[l])
Thuật toán gradient descent cần tính dW[l]dW^{[l]}dW[l] và db[l]db^{[l]}db[l] ở mỗi lớp để có thể update W[1],b[1],...W^{[1]}, b^{[1]}, ...W[1],b[1],.... Backward propagation theo đúng tên gọi của nó đi từ output layer →
ightarrow→ hiddenlayer →
ightarrow→ input layer, và dựa vào các giá trị của z[l]z^{[l]}z[l] và a[l]a^{[l]}a[l] đã tính toán ở mỗi lớp trong forward propagation mà tính được dW[l]dW^{[l]}dW[l] và db[1]db^{[1]}db[1]
 Dưới đây tôi sẽ trình bày công thức tính, phần chứng minh sẽ để ở bài kế tiếp
Dưới đây tôi sẽ trình bày công thức tính, phần chứng minh sẽ để ở bài kế tiếp
Back propagation cho 1 training example
Đạo hàm của zzz ở lớp cuối cùng dz[L]=y^−ydz^{[L]} = hat y - ydz[L]=y^−y Với mỗi lớp l dz[l]=da[l]∗g[l]′(z[l])dz^{[l]} = da^{[l]} * g^{[l]'}(z^{[l]})dz[l]=da[l]∗g[l]
