Spectral clustering và bài toán tìm kiếm cộng đồng ẩn (Phần 1/2)

Trong phần này, tôi xin giới hạn chỉ giới thiệu về thuật toán Spectral clustering và mô hình giải quyết bài toán. Phần demo và hướng dẫn chi tiết xin hẹn ở phần tiếp theo.

Trong thống kê đa biến và phân cụm dữ liệu, kỹ thuật spectral clustering cho phép tận dụng giá trị đặc trưng của ma trận tương tự với dữ liệu lớn để thực hiện giảm chiều trước khi chia thành các kích thước nhỏ hơn. Đầu vào là ma trận tương tự bao gồm định lượng giống nhau tương đối của mỗi cặp trong tập dữ liệu.

Mục tiêu của thuật toán này là:

• Xử lý phân nhóm tương tự như phân vùng đồ thị mà không sử dụng các giả định về hình thức của các cụm.
• Nhóm chỉ sử dụng các vector riêng của ma trận được lấy từ các dữ liệu có sẵn.
• Kết nối dữ liệu đến một không gian ít chiều hơn sau khi được tách ra để có thể dễ dàng xử lý tiếp.

Trong toàn bài viết, mình sẽ sử dụng ví dụ với mạng sau:

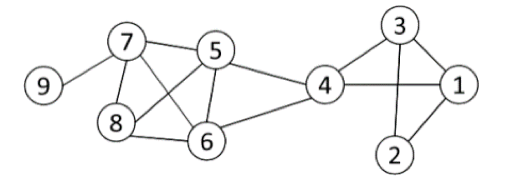
Để hiểu được thuật toán, trước tiên ta cần tìm hiểu về Adjacency Matrix (A), Degree Matrix (D), Cut và K-means.

Adjacency Matrix (A)

A là ma trận NxN nhị phân đối xứng. Các cột và các hàng tiêu biểu cho các đỉnh, đầu vào tiêu biểu cho các cạnh của đồ thị. Ma trận có đường chéo là 0. A(i,j) = 0 nếu i, j không có kết nối. A(i,j) = 1 nếu i, j có kết nối.

Ví dụ: trong mạng ví dụ đã nêu ở đầu bài ta có:

Degree Matrix (D)

D là ma trận NxN đối xứng mà bao gồm thông tin về bậc của các đỉnh. Bậc d(vi) của đỉnh vi trong đồ thị là số cạnh gắn liền của đỉnh. D(i,j) = 0 nếu i≠j. D(i,j) = d(vi) nếu i=j → D = diag(d1,d2, … ,dn).

VD: Trong mạng hình ví dụ:

D = diag(3,2,3,4,4,4,4,3,1)

Cut.

Có thể dễ dàng nhận thấy rằng: trong một mạng có nhiều nhóm nhỏ, phần lớn sự tương tác là ở bên trong nhóm, còn tương tác giữa các nhóm là rất ít. Cut là sự phân chia của các đỉnh đồ thị thành hai bộ phận. Chính thế có thể nói bài toán phát hiện cộng đồng là tập hợp các bài toán tối thiểu về cut.

Minimum cut problem (bài toán cắt cực tiểu): tìm một sự phân chia đồ thị như là số cạnh giữa hai phần là nhỏ nhất. Cắt cực tiểu thường trả lại một phân vùng thiếu cân bằng với một phần là duy nhất. Có thể thay đổi khách quan để cân nhắc độ lớn của cộng đồng. Có các loại cut:

• RatioCut

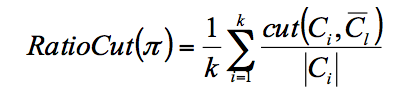
• NormalizedCut

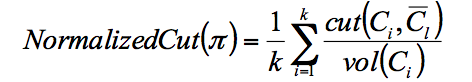
vol(Ci) là tổng tất cả các cạnh của mỗi nút.

Ví dụ: Trong mạng ví dụ, ta sẽ thực hiện cắt 2 đường như sau:

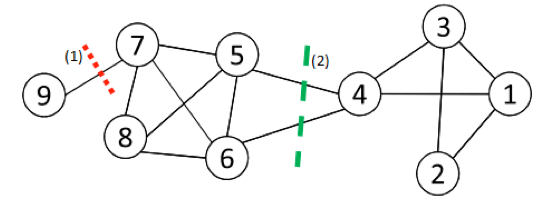
Với đường cut (1):

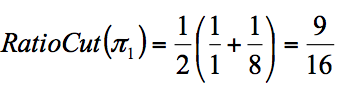
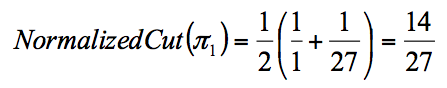
Với đường cut (2):

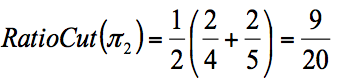
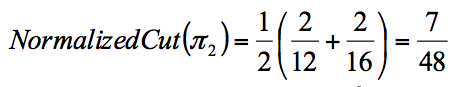
Cả Ratio và Normalized Cut đều đưa ra phân vùng cân bằng với (1), tuy nhiên chỉ Ratio đưa ra vùng cân bằng ở (2).

K-means

K-Means là thuật toán rất quan trọng và được sử dụng phổ biến trong kỹ thuật phân cụm. Tư tưởng chính của thuật toán K-Means là tìm cách phân nhóm các đối tượng (objects) đã cho vào K cụm (K là số các cụm được xác đinh trước, K nguyên dương) sao cho tổng bình phương khoảng cách giữa các đối tượng đến tâm nhóm (centroid) là nhỏ nhất.

Spectral clustering

Cả ratio cut và normalized cut đều có thể được đưa vào công thức như:

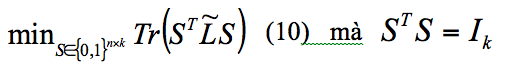
Trong đó:

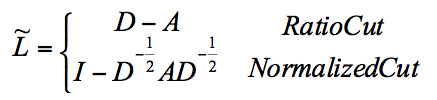
Giải pháp: S là vector riêng của L với giá trị riêng nhỏ nhất (trừ trường hợp đầu tiên). Sau đó áp dụng k-means cho S, ta được cộng đồng cần tìm.

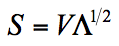
Trong đó:

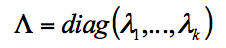
V là vector riêng.

Áp dụng vào trong mạng ví dụ:

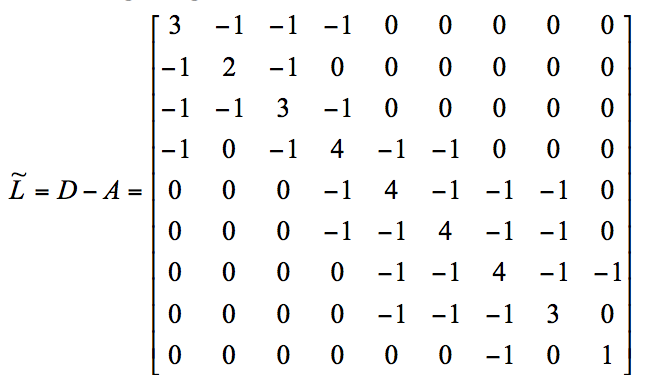
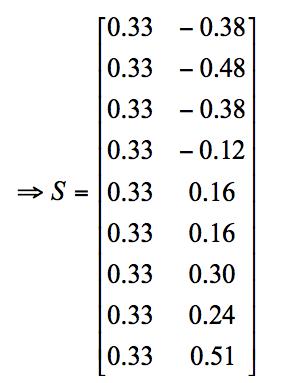
Áp dụng K-means ta được 2 cộng đồng: {1,2,3,4},{5,6,7,8,9}