Bài toán tháp Hà Nội: Sử dụng đệ quy để giải - Giải thuật đệ quy

Trong bài này mình sẽ thực hiện giải một bài toán rất kinh điển đó chính là bài toán tháp Hà Nội.

Đây là một bài toán áp dụng đệ quy để giải, có lẽ các bạn cũng đã từng nghe qua bài toán này rồi. Và chúng ta sẽ lần lượt tìm hiểu về bài toán tháp Hà Nội là gì? Sau đó mình sẽ đưa ra giải thuật để giải.

Bài toán tháp Hà Nội là gì?

Bài toán tháp Hà Nội là một trò chơi toán học rất phổ biến. Nó đơn giản chỉ là việc dịch chuyển các đĩa từ cột này sang cột khác. Nhưng để thành thạo luật chơi của nó thì rất khó.

Luật chơi được mô tả như sau:

Trò chơi này gồm một bộ các đĩa kích thước khác nhau, có lỗ ở giữa, nằm xuyên trên ba cái cột. Bài toán đố bắt đầu bằng cách sắp xếp các đĩa theo trật tự kích thước vào một cột, sao cho đĩa nhỏ nhất nằm ở trên cùng, tức là tạo thành một hình nón.

Yêu cầu của trò chơi là di chuyển toàn bộ số đĩa sang một cột khác, tuân theo các quy tắc sau:

• Một lần chỉ có 3 cột để di chuyển
• Chỉ di chuyển một đĩa trên cùng (không được di chuyển đĩa nằm giữa hay nằm cuối).
• Một đĩa chỉ có thể đặt lên một đĩa lớn hơn (không nhất thiết hai đĩa này phải có kích thước liền kề, tức là đĩa nhỏ nhất vẫn có thể đặt trên đĩa lớn nhất).

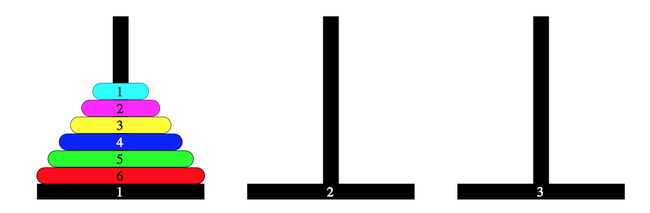
Ý tưởng đệ quy

Dựa vào luật chơi của trò chơi, chúng ta sẽ áp dụng nó vào đệ quy để giải bài toán này bằng ngôn ngữ C++ nhé.

Trong bài toán này chúng ta cần quan tâm 4 vấn đề: số đĩa N, cột A, cột B, cột C.

Nhiệm vụ của chúng ta là chuyển N số đĩa từ cột A sang cột C, lấy cột B làm cột tạm.

Ý tưởng:

• Nếu đã biết cách chuyển N - 1 đĩa từ cột A sang cột B, ta chỉ cần chuyển đĩa thứ N (đĩa cuối cùng) từ cột A sang cột C, rồi chuyển N - 1 đĩa từ cột B sang cột C.
• Giải thuật không còn đệ quy khi chỉ có 1 đĩa, vì ta chuyển trực tiếp từ cột A sang cột C luôn mà không cần thông qua cột B.
• Độ phức tạp của nó là: 2n - 1 (lần dịch chuyển).

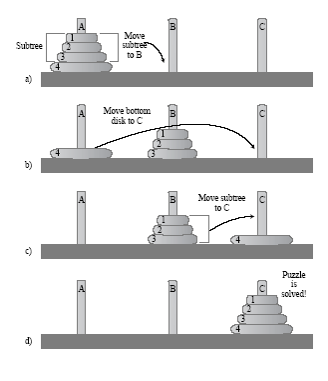
Giải bài toán tháp Hà Nội bằng C++

Chúng ta đã có ý tưởng giải bài toán, chỉ cần dựa vào đó và áp dụng thêm kiến thức về đệ quy để bắt tay vào việc giải thôi nào.

Giải thuật

void move(int n,char A,char B,char C)
 {
      if(n==1){
        cout<<A<<" ==> "<<C<<"
";// nếu n = 1 thì dịch chuyển từ A -> C
      }
      else {		
        // Nếu n > 1 thì thực hiện lần lượt các bước
        move(n - 1, A, C, B); // 1. Dịch chuyển n-1 đĩa từ A -> B
        cout<<A<<" ==> "<<C<<"
"; // 2. Dịch chuyển đĩa thứ n từ A -> C
        move(n - 1, B, A, C); // 3. Dịch chuyển n-1 đĩa từ B -> C
      }
 }

Như các bạn thấy chúng ta cần truyền 4 tham số cho hàm move() là: số đĩa n, cột A, cột B, cột C.

Nếu như n == 1 (chỉ có một đĩa) thì chúng ta chỉ cần chuyển đĩa đó từ cột A sang cột C là xong.

Trường hợp số đĩa n lớn hơn 1 thì chúng ta cần thực hiện dịch chuyển ba lần:

1. Chuyển n - 1 đĩa từ cột A sang cột B -> move(n - 1, A, C, B);
2. Chuyển đĩa còn lại (đĩa thứ n) từ cột A sang cột C -> cout<<A<<" ==> "<<C<<" ";
3. Chuyển n - 1 đĩa từ cột B sang cột C -> move(n - 1, B, A, C);

Giả sử chúng ta có n = 3 thì số lần thực hiện dịch chuyển bằng 2n - 1 = 23 - 1 = 7 (lần).

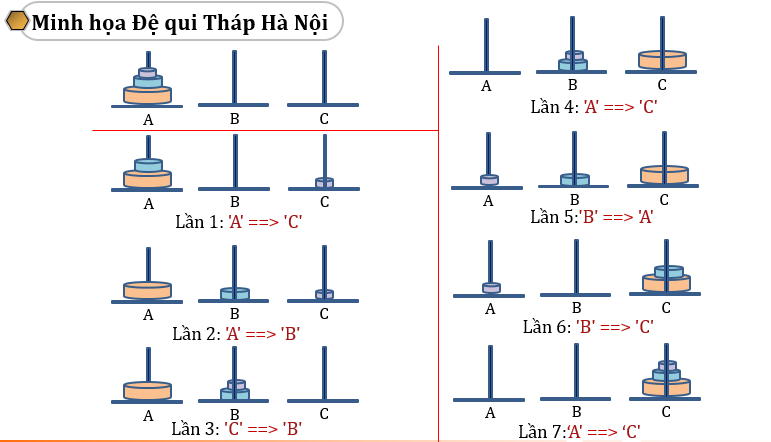
Hàm main()

#include <iostream>
using namespace std;

void move(int n,char A,char B,char C)
 {
      if(n==1){
        cout<<A<<" ==> "<<C<<"
";// nếu n = 1 thì dịch chuyển từ A -> C
      }
      else {		
        //// Nếu n > 1 thì thực hiện lần lượt các bước
        move(n - 1, A, C, B); // 1. Dịch chuyển n-1 đĩa từ A -> B
        cout<<A<<" ==> "<<C<<"
"; //2. Dịch chuyển đĩa thứ n từ A -> C
        move(n - 1, B, A, C); // 3. Dịch chuyển n-1 đĩa từ B -> C
      }
 }

int main() {
  int n;
  cout<<endl<<"Nhập vào số đĩa N mà bạn muốn tìm cách giải: ";
  cin>>n;
  cout<<"Thứ tự dịch chuyển các vị trí A B C là: 
";
  move(n, 'A', 'B', 'C');
  
  cout<<"
------------------------------
";
  cout<<"Chương trình này được đăng tại Zaidap.com.net";
}

Kết quả:

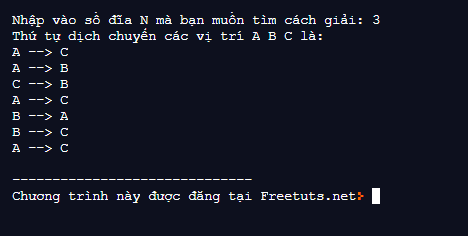
Như vậy là chúng ta đã thực hiện xong chương trình tìm cách giải của trò chơi tháp Hà Nội. Chúc các bạn thực hiện thành công!!!