Đệ quy nhị phân (Binary Recursion) - Giải thuật đệ quy

Trong bài này mình sẽ giới thiệu đến các bạn một trong các hàm đệ quy tiếp theo đó là đệ quy nhị phân (Binary Recursion).

Đây là một hàm đệ quy khá phổ biến trong quá trình xử lý về tìm kiếm, sắp xếp, các phép toán trên cây.

Chúng ta sẽ tìm hiểu về đệ quy nhị phân là gì? Cơ chế hoạt động của nó ra sao? Các bạn cùng mình tìm hiểu nhé.

1. Đệ quy nhị phân là gì?

Đệ quy nhị phân là dạng đệ quy gọi hai lần chính nó. Hiểu đơn giản là trong một hàm đệ quy, mà có dòng lệnh gọi chính hàm đó hai lần.

Ta có một hàm tìm dãy số Fibonacci sử dụng đệ quy như sau:

int fib(int n){
if(n <= 2) return 1; // điểm dừng
return fib(n - 1) + fib(n - 2);
} 

Một hàm tương tự như trên được gọi là hàm đệ quy nhị phân, trong hàm fib() gọi chính nó hai lần để tính.

2. Cơ chế của đệ quy nhị phân

Để biểu diễn cơ chế của hàm đệ quy nhị phân ta có hai cách biểu diễn. Cách thứ nhất là biểu diễn bằng Stack và cách thứ hai là biểu diễn bằng cây (đây là cách thường được sử dụng nhất).

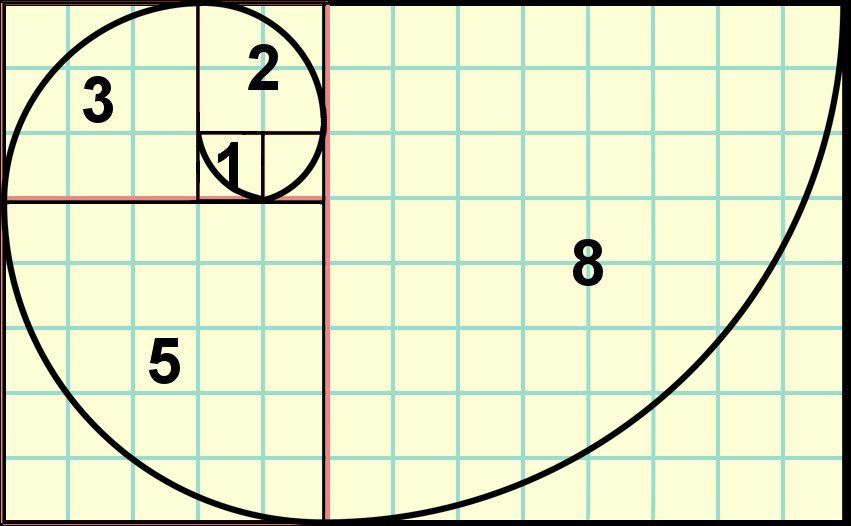
Trong phần này mình sẽ biểu diễn cơ chế hoạt động của đệ quy nhị phân bằng cây. Chúng ta sẽ lấy bài toán tìm số fibonacci thứ n (với n được nhập từ bàn phím).

Để làm được bài toán chúng ta cần hiểu được số fibonacci là số như thế nào?

Theo wikipedia thì dãy số fibonacci là dãy vô hạn các số tự nhiên bắt đầu bằng hai phần tử 0 1 hoặc 1 1. Các phần tử sau đó được thiết lập theo quy tắt mỗi phần tử luôn bằng tổng hai phần tử trước nó.

Công thức của nó là:

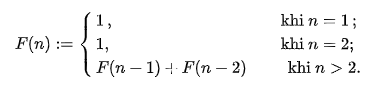
Ta có hàm fib() sử dụng đệ quy nhị phân để tìm số fibonacci thứ n như sau:

int fib(int n){
  if(n <= 2) return 1;
  return fib(n - 1) + fib(n - 2);
}

Giả sử chúng ta cần tìm số fibonacci ở vị trí 6 (fib(6)), khi đó cơ chế hoạt động được biểu diễn dưới dạng cây của nó như sau:

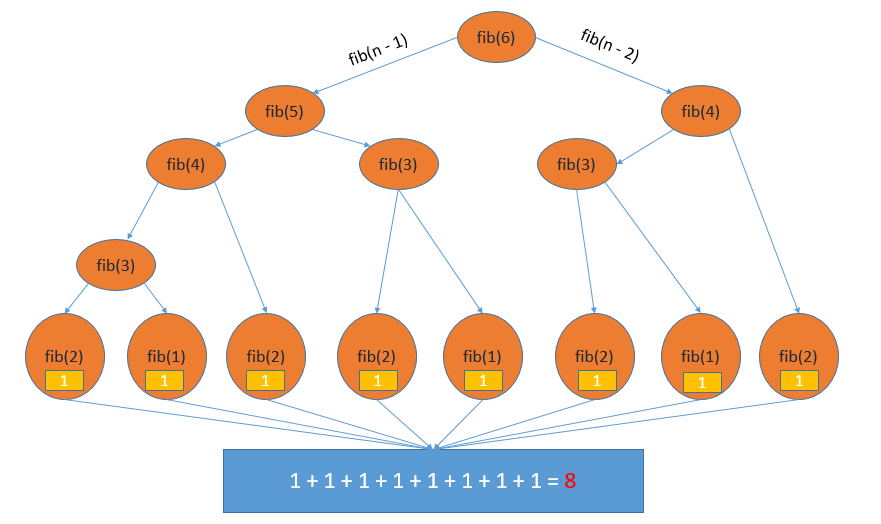
Điểm dừng trong hàm đệ quy trên chính là n <= 2, vì vậy fib(2) và fib(1) sẽ return 1. Sau khi hàm kết thúc, kết quả bằng tổng các fib(1) và fib(2) là 8, đây chính là giá trị của vị trí số 6 trong dãy fibonacci.

Các bạn có thể vẽ cây biểu diễn cho fib(7), fib(8), … để có thể hiểu được bài. Nếu các bạn thực hành bằng tay nhiều điều đó giúp các bạn nhớ rất lâu, hãy cố gắng luyện tập nhé.

Code mẫu:

#include <iostream>
using namespace std;

int fib(int n){
  if(n <= 2) return 1;
  return fib(n - 1) + fib(n - 2);
}

int main() {
  int kq,n;
  cout<<"Nhập vị trí n muốn tìm trong dãy fibonacci: ";
  cin>>n;
  kq = fib(n);
  cout<<"
Số fibonacci ở vị trí "<<n<<" là: "<<kq;
  cout<<"
-----------------------------------
";
  cout<<"Chương trình này được đăng tại Zaidap.com.net";
}

Kết quả:

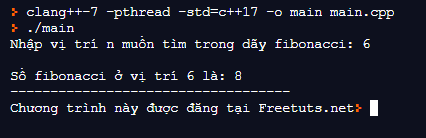
3. Kết luận

Như vậy là chúng ta đã tìm hiểu về khái niệm đệ quy nhị phân, cơ chế hoạt động của nó trong C++ thông qua ví dụ tìm vị trí của số n trong dãy fibonacci. Qua bài này mình muốn các bạn nắm rõ được cơ chế hoạt động của đệ quy nhị phân. Bởi vì đây là một hàm rất quan trọng để áp dụng cho sắp xếp, tìm kiếm, … Các bạn có thể tìm hiểu thêm các bài tập C++.