huật toán tìm ước chung lớn nhất trong C/C++ - huật toán căn bản

Trong bài này chúng ta sẽ tìm hiểu thuật toán tìm ước chung lớn nhất trong C++, bằng cách sử dụng vòng lặp, thuật toán Euclid và thuật toán loại trừ.

Đề bài: Nhập vào 2 số nguyên A và B, viết chương trình tìm ứng chung lớn nhất của 2 số đó.

Kết quả:

Input  :  A = 20, B = 12
Output :  4

Có rất nhiều cách để giải quyết bài toán này, trong bài viết chúng ta sẽ đi qua 3 cách để triển khai bài toán. Từ đó, lựa chọn ra cách tối ưu nhất.

1. Tìm UCLN sử dụng vòng lặp

Đây là cách đơn giản nhất để cài đặt thuật toán tìm UCLN. Đối với thuật toán này chúng ta sẽ đi lặp lần các giá trị từ min(A, B) về 0 và kiểm tra giá trị một.

Các bước triển khai thuật toán này sẽ như sau: Chúng ta sẽ sử dùng vòng lặp for đẻ giải quyết bài tòán này.

• Lặp từ min(A,B) về 0.
• Với mỗi vòng lặp kiểm tra A và B có chia hết cho i hay không? Nếu chia hết trả về i.

Trình bài bài toán với ngôn ngữ C/C++ sẽ như sau :

#include <bits/stdc++.h>
using namespace std;

//Hàm tìm ước chung lớn nhất
int UCLN(int A, int B) {
    for(int i = min(A, B); i > 0; --i) {
        if (A % i == 0 && B % i ==0)
            return i;
    }
    //Không chạy tới đây vì A, B luôn chia hết cho 1
}
int main() {
    int A,B;
    A = 20;
    B = 12;
    cout << UCLN(A, B);
}

Output: 4

Đây là cách đơn giản nhất để giải quyết bài toán này, nhưng đối với dữ liệu lớn việc xử lý bằng cách này không hoàn toàn tối ưu. Độ phức tạp của thuật toán này là O(min(A, B)).

2. Tìm UCLN bằng phương pháp trừ

Ý tưởng của thuật toán này là trừ hai số A và B cho nhau tới khi hai số này bằng nhau. Lúc này ta sẽ tìm được ƯCLN của 2 số. Các bước triển khai thuật toán sẽ như sau:

• Kiểm tra liệu rằng A hoặc B có bằng 0 hay không ? Nếu bằng 0 trả về ƯCLN là A+B. Dừng chương trình.
• Lặp cho tới khi A = B. Với mỗi vòng lặp thì biến biến max(A, B) = giá trị max(A, B) - giá trị min(A, B).

Trình bài bài toán với ngôn ngữ C/C++ sẽ như sau :

#include <bits/stdc++.h>
using namespace std;

//Hàm tìm UCLN
int UCLN(int A, int B) {
    //Nếu A hoặc B = 0 thì UCLN = A+ B
    if (A == 0 || B == 0)
        return A + B;

   //Lặp cho tới khi A = B
    while(A != B) {
        //Lấy số lớn trừ số bé.
        if (A > B) {
            A -= B;
        }else{
            B -= A;
        }
    }
    
   // Trả về UCLB
   // Lúc này A = B nên return về A hay B đều giống nhau
    return A;
}
int main() {
    int A,B;
    A = 20;
    B = 12;
    cout << UCLN(A, B);
}

Output: 4

Thuật toán sẽ thực hiện lần lượt các bước như sau. Giả sử A = 100, B = 30.

100 =  100  - 30
70 = 70 - 30
40 = 40 - 30
//Đến đây là B < A nên nó sẽ lấy B = B - A
30 = 30 - 10
20 = 20 - 10
A = B = 10
reutrn 10

Ngoài thực hiện trừ A và B, chúng ta có thể thay dấu trừ thành chia dư. Kết quả trả về tương tự.

int UCLN(int A, int B) {

    while(A * B != 0) {
        if (A > B) {
            A %= B;
        }else{
            B %= A;
        }
    }
    return A + B;
}

Đây là thuật toán tối ưu hơn so với thuật toán ban đầu, nhưng đây chưa phải là thuật toán tối ưu nhất.

3. Tìm UCLN sử dụng thuật toán Euclid

Giải thuật Euclid, hay Thuật toán Euclid, là một giải thuật giúp tính ước số chung lớn nhất (ƯSCLN) của hai số một cách hiệu quả. Trong phần này chúng ta sẽ đề cập giải thuật ở 2 khía cạnh cơ bản và mở rộng.

Thuật toán Euclid

[Thuật toán Euclid] là một giải thuật giúp chúng ta tìm ước chung lớn nhất của 2 số. Nó được triển khai dựa trên tính chất của UCLN đó là UCLN(A, B) = UCLN(B, A%B).

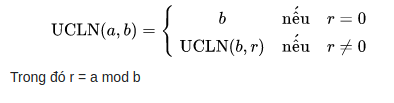
Giả sử chúng ta có 2 số A = 20, B = 12. Triển khai bằng thuật toán Euclid sẽ hoạt động như sau.

UCLN(20, 12) = UCLN(12, 20%12) = UCLN(12, 8)
UCLN(12, 8) = UCLN(8, 12%8) = UCLN(8, 4)
UCLN(8, 4) = UCLN(4, 8%4) = UCLN(4, 0)
Vì B = 0 nên UCLN(4, 0) sẽ là 4

Ý tưởng triển khai thuật toán này sẽ quy nạp cho tới khi A % B = 0. Trình bài bài toán với ngôn ngữ C/C++ sẽ như sau :

#include <bits/stdc++.h>
using namespace std;

int UCLN(int A, int B) {
    if (B == 0)
        return A;
    return UCLN(B, A%B);
}
int main() {
    int A,B;
    A = 20;
    B = 12;
    cout << UCLN(A, B);
}

Output: 4

Đây là cách tối ưu nhất để giải các bài toán với dữ liệu lớn. Độ phực tạp của thuật toán này là O(logmax(A,B)).

Thuật toán Euclid mở rộng (Extended Euclidean algorithm)

UCLN(A, B) có một tính chất khá đặc biệt đó là luôn biểu diễn được ở dạng Ax + By = UCLN(A, B) trong đó x, y là hai số nguyên. Đây là một phần mở rộng của thuật toán Euclid cho phép chúng ta tìm ra hai số x và y thỏa mãn tính chất.

#include <bits/stdc++.h>

using  namespace std;
int d, x, y;
void extendedEuclid(int A, int B) {
    if (B == 0) {
        d = A;
        x = 1;
        y = 0;
    }
    else {
        extendedEuclid(B, A%B);
        int temp = x;
        x = y;
        y = temp - (A/B)*y;
    }
}

int main() {
    extendedEuclid(16, 10);
    cout << "UCLN(16, 10) = " << d << endl;
    cout << "x, y: " << x <<  ", " << y << endl;
    return 0;
}

Output: UCLN(20, 12) = 4
        x, y: -1, 2

Độ phức tạp của thuật toán này là O(log(max(A,B)).

4. Tìm UCLN bằng hàm có sẵn trong C/C++

Ngoài cách tự viết các hàm tìm uớc chung lớn nhất, chúng ta còn có thể sử dụng hàm __gcd có sẵn trong thư viện algorithm của C/C++.

#include<iostream>
#include<algorithm>
using namespace std;
int main() {
    int A,B;
    A = 20;
    B = 12;
    cout << __gcd(A, B);
}

Output: 4

Đây là cách nhanh nhất để giải bài toán trong C/C++, ngoài tìm ước chung lớn nhất thư viện algorithm còn có nhiều hàm hỗ trợ khác cho giải các bài toán như max, min, sort,...Chúng ta có thể tham khảo thêm về thư viện algorithm.

Trên đây là phần giới thiệu cũng như triển khai của các thuật toán tìm ước chung lớn nhất. Đây cũng là những thuật toán hay được sử dụng cũng như rât hữu ích trong quá trình giải các bài toán tìm kiếm. Rất mong bài viết sẽ hữu ích cho bạn !