hụât toán tìm kiếm nhị phân (Binary Search) - Sắp xếp & tìm kiếm

Trong bài viết này chúng ta sẽ tìm hiểu về thuật toán tìm kiếm nhị phân (Binary search). Đây là thụât toán phổ biến để tìm kiếm vị trí một phần tử trong một mảng đã sắp xếp.

Để bài: Cho một danh sách arr[] đã được sắp xếp gồm n phần từ , viết một hàm đưa ra vị trí của phần từ x trong mảng.

Ví dụ:

Input : arr[] = {15, 20, 25, 30, 31, 44, 66}
        x = 25;
Output : 2

Một cách tìm kiếm đơn giản hơn rất nhiều đó là thụât toán tìm kiếm tuần tự (linear search) nhưng độ phức tạp khá lớn lên tới O(n), không khả thi để thực hiện tìm kiếm trên một mảng lớn. Để giải quyết bài toán này chúng ta sẽ sử dụng thụât toán tìm kiếm nhị phân (binary search) được giới thiệu bên dưới.

1. Tìm kiếm nhị phân (Binary Search)

Thụât toán tìm kiếm nhị phân (Binary Search) hay còn được gọi là tìm kiếm một nửa là thụât toán tiếp kiếm được sử dụng rất nhiều trong thực tế cho phép tìm kiếm vị trí của một phần tử trong một mảng đã được sắp xếp.

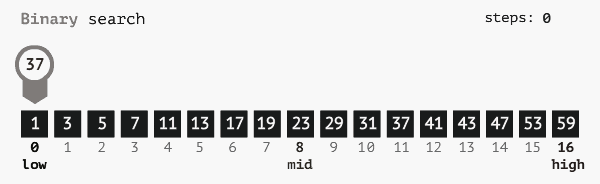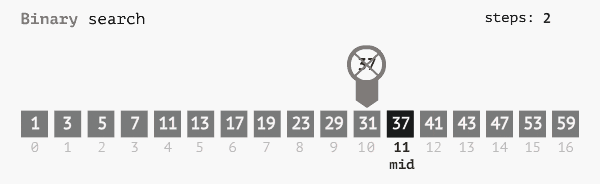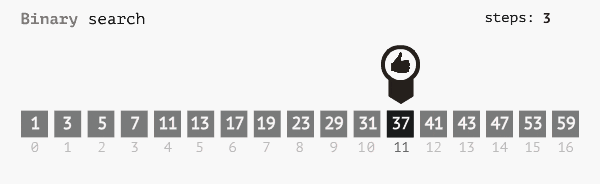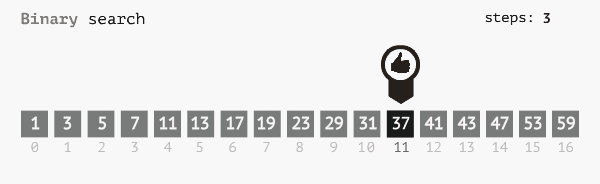
Thụât toán tìm kiếm nhị phân thực hiện tìm kiếm một mảng đã sắp xếp bằng cách liên tục chia các khoảng tìm kiếm thành 1 nửa. Bắt đầu với một khoảng từ phần tử đầu mảng, tới cuối mảng. Nếu giá trị của phần tử cần tìm nhỏ hơn giá trị của phần từ nằm ở giữa khoảng thì thu hẹp phạm vi tìm kiếm từ đầu mảng tới giửa mảng và nguợc lại. Cứ thế tiếp tục chia phạm vi thành các nửa cho dến khi tìm thấy hoặc đã duyệt hết.

Thuật toán tìm kiếm nhị phân tỏ ra tối ưu hơn so với tìm kiếm tuyết tính ở các mảng có độ dài lớn và đã được sắp xếp. Ngược lại, tìm kiếm tuyến tính sẽ tỏ ra hiệu quả hơn khi triển khai trên các mảng nhỏ và chưa được sắp xếp.

2. Ý tưởng triển khai thụât toán

Thuật toán tìm kiếm nhi phân là một thuật toán khá thông dụng và chỉ dùng được với một mảng đã sắp xếp. Để triển khai thuật toán này hãy chắc chắn rằng mảng đã được sắp xếp. Sau đây là ý tưởng triển khai thuật toán.

• Xét một đoạn trong mảng arr[left...right]. Lúc này giá trị của left và right lần luợt là 0 và số phần tử của mảng - 1.
• So sánh x với phần tử nằm ở vị trí chính giữa của mảng (mid = (left + right) /2). Nếu x bằng arr[mid] thì trả về vị trí và thoát vòng lặp.
• Nếu x < arr[mid] thì chắc chắn x sẽ nằm ở phía bên trái tức là từ arr[left....mid-1].
• Nếu x > arr[mid] thì chắc chắn x sẽ nằm ở phía bên phải mid tức là ở khoảng arr[mid+1...right].
• Tiếp tục thực hiện chia đôi các khoảng tìm kiếm tới khi nào tìm thấy được vị trí của x trong mảng hoặc khi đã duyệt hết mảng.

Người ta đã chứng minh được độ phực tạp của thụât toán tìm kiếm nhi phân trong trường hợp tốt nhất là O(1), trong trường hợp xấu nhất là O(log2n) và trung bình cũng là O(log2n). Tuy nhiên, ta không nên quên rằng trước khi sử dụng tìm kiếm nhị phân, dãy khoá phải được sắp xếp rồi, tức là thời gian chi phí cho việc sắp xếp cũng phải tính đến.

3. Triển khai thụât toán

Sau đây là các bước triển khai thuật toán, các bước thực hiện đều được comment ở từng đoạn.

#include <bits/stdc++.h>
using namespace std;

//Hàm tìm kiếm nhi phân
int binarySearch(int arr[], int left, int right, int x) {
    int middle;

    while(left <= right) {
        // Lấy vị trí ở giữa left và right
        middle = (left + right) / 2;

        // Nếu phần từ ở giữa bằng x thì trả về
        // vị trí
        if (arr[middle] == x)
            return middle;

        // Nếu x lớn hơn phần tử ở giữa thì
        // chắc chắn nó nằm bên phải.
        // Chỉ định left phần từ ở giữa + 1
        if (x > arr[middle])
            left = middle + 1;
        else
            //Ngược lại
            right = middle - 1;
    }

    //Trả về -1 nếu không tìm thấy gía trị trong mảng.
    return -1;
}
int main() {
    int arr[] = {15, 20, 25, 30, 31, 44, 66};

    //Lấy ra độ dài của mảng
    int n = sizeof(arr) / sizeof(arr[0]);
    //Phần từ cần tìm
    int x = 25;
    
    // n -1 là vị trí cuối cùng trong mảng.
    int result = binarySearch(arr, 0, n-1, x);

    cout << result;
}

Khởi chạy chươn trình chúng ta sẽ nhận được kết quả là vị trí của 25 trong mảng.

Output : 2

Trên đây là phần giới thiệu cũng như triển khai của thụât toán tìm kiếm nhị phân. Đây cũng là một thuật toán hay được sử dụng cũng như rât hữu ích trong quá trình giải các bài toán tìm kiếm. Rất mong bài viết sẽ hữu ích cho bạn !