30/09/2018, 17:23
Hỏi về bản đồ Karnaught trong toán rời rạc?
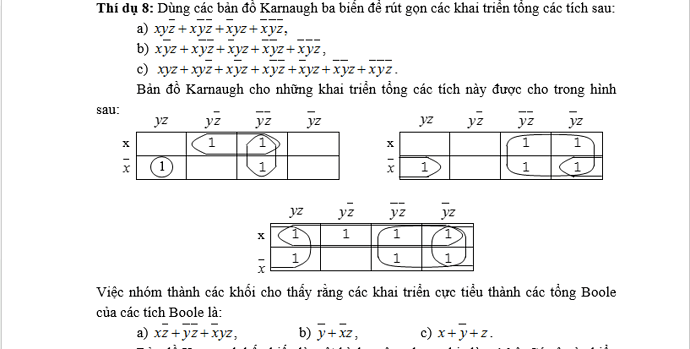
Mình đang học toán rời,có chỗ này bài a mình không hiểu lắm mọi người giải thích hộ mình với,mình lập được bảng nhưng không biết rút gọn ra biểu thức thu gọn,ví dụ câu a. Cám ơn mọi người.
Bài liên quan






những ô kề nhau thì rút gọn với nhau được, ví dụ: ô xyz’ và xy’z’ rút gọn thành xz’, biến nào thay đổi thì rút gọn, biến nào không thay đổi thì giữ lại. 1 ô thì không rút gọn được biến nào, 2 ô thì rút được 1 biến, 2^n ô thì rút gọn được n biến
uh em hieu roi nhưng em có 1 thắc mắc là mình biết chọn ô nào để rút gọn nhỉ ?
những ô đánh số 1, câu a là xyz’,xy’z’,x’yz,x’y’z’, nói chung là những tích có trong biểu thức. Nó bằng 1 thì biểu thức bằng 1
chọn những ô kề nhau, tất cả ô đánh số bằng 1 phải được chọn ít nhất 1 lần, có thể chọn nhiều lần
giải thích dùm em câu b tại sao lại ra như vậy nhỉ?
em chú ý mấy số mà người ta khoanh lại, mỗi một vòng là một số hạng sau khi được rút gọn.
Chú ý là cột đầu tiên và cột cuối cùng được xem là 2 cột kề nhau
chọn 2 với 4 ô thôi bạn à .cứ gộp các ô đủ 4 ô thì lấy .nếu không chỉ lấy 2 ô thôi
ak thì ra là thế hèn gì thấy nó là lạ :3
mà anh ơi cho em hỏi nếu mình lấy 1 ô thu gọn với ô kề bên phải nó thì có dc lấy tiếp ô đó đi thu gọn với ô kề dưới nó ko anh nhỉ ?
cái này ứng dụng trong điện tử số!!! (nhiều cái # nữa )
very quan trọng
bởi vậy em mới học nên còn ngu muội -_-
Lấy mấy lần cũng được, miễn là không bị lặp lại
zay là em làm dc roi :)) thank anh nhiều <3
mà anh ơi,thứ tự các cột với hàng bắt buộc phải ghi zay hả anh,mà đảo lộn thứ tự các cột với hàng dc ko anh
bạn làm quen thì sẽ chọn ra ô khoang nhanh thôi. còn không thì có thuật toán luôn, cuối cùng cũng ra đa thức tối tiểu.
miễn nó biểu diễn được tất cả trường hợp là được, nhưng mà nên ghi theo chuẩn như trên.
nhưng neu em ko ghi theo thứ tự cột hàng trên kia thì nó ra kết qảu khác
Thứ nhất: Bìa Karnaught có tính chất các ô liền kề nên bạn phải chú ý ghi cho đúng thứ tự 00 01 11 10 (0 là x(ngang), 1 là x) không được đảo thứ tự của 2 tổ hợp bất kỳ.
Thứ 2: các ô ở cạnh trái liền kề với ô cạnh phải, ô cạnh dưới liền kề với ô cạnh trên, 4 góc liền kề với nhau nên để ý khoanh ô liền kề cho đúng.
Thứ 3: Khoanh 1, 2, 4 hoặc 8 ô liền kề nhau. Không khoanh 3, 5, 6 ô.
Thứ 4: Khoanh những ô có ít sự lựa chọn trước, đó là những ô bị cô lập. Tìm cách nhóm những ô đó với các ô liền kề sao cho được nhiều ô nhất. Làm cách này sẽ giúp bạn tránh bị lặp vòng.
Thứ 5: trong một ô lớn đã khoanh, đi từ trái qua phải bit nào không bị đổi (đổi từ 0 sang 1 hoặc 1 về 0) thì ghi lại.
Xét 4 ô liền kề nhau thì trả lại 1 biến chung. 2 ô liên tiếp thì trả về biến chung. làm từ ô có ít khả năng tối thiểu nhất. Nếu không cần thiết tối thiểu có thể bỏ qua nhưng ô tối thiểu nhiều lần
///////////////////////////
Nhân đây cho em hỏi cùng chuyên mục. với hàm Bool có n biến (n>4) thì tối thiểu như thế nào ạ
Mình vừa thi môn này xong :D. Cái bảng này thì 4 ô liên tiếp nhau tạo thành hình vuông hoặc hình chữ nhật thì sẽ có 1 biến chung… 2 ô liên tiếp nhau thì có 2 biến chung…
với n = 5 thì làm 2 bảng cho 4 biến ghép lại. Còn trên 5 biến thì có thể tìm hiểu kĩ thuật tối thiểu hóa Quine-McCluskey