01/10/2018, 13:47
Làm sao để tìm tập con các chữ số trong dãy gồm n số fibonacci bắt đầu từ vị trí i và chia hết cho k
bo_de_hsg_quoc_gia_tin_hoc_2017.pdf
432.63 KB
Chào các anh,chị. Em được thầy giáo của em chỉ em qua web diễn đàn này để tiện hỏi về tin. Do e thi hsg tin . Thực ra e mới lớp 8 và thầy đã cho đề bài thế này
Và cũng cho em mạo tí là em hỏi về pascal
Hãy tìm các số có trong dãy số Fibonacci từ 1 đến n với n>2.
Và bộ đề gốc thì nó nằm ở link trên
Bài liên quan






Đề cho ai cần:
Cho một tập n số Fibonacci liên tiếp nhau. Hỏi rằng có thể tìm được một tập con các số trong n số Fibonacci kia, bắt đầu từ số thứ i, sao cho tổng của chúng chia hết cho một số nguyên dương k ( k <= n) cho trước hay không? Nhắc lại, một tập con q số của một dãy n số là một cách chọn ra q số bất kỳ trong n số của dãy đó, mỗi số được chọn không quá một lần.
Input
Dòng đầu là số testcase T (T <= 10)
T dòng tiếp theo là 3 số lần lượt n, i, k
Output
Gồm T dòng, mỗi dòng ghi q số được chọn theo thứ tự trong dãy Fibonacci. Nếu không tìm được in ra 0
Ràng buộc
Vd:
Đang rảnh rỗi nên tiện giúp ghi đề lại luôn.
Hi Nghĩa.
Theo mình bạn có thể giải theo 2 cách.
Mới lớp 8 mà chơi đề ác quá Nói thật chứ thi HSG cấp 2 chỉ thi đến loang và có chút chút QHĐ thôi, ôn gì ác quá, không tốt cho trẻ nhỏ.
Nếu em muốn hỏi chuyên về giải thuật, hãy tìm đến group VNOI trên fb. Ít nhất là trên đó đề QG được bàn tán rất sôi nổi.
Đặt=%5Csum_%7Bi=1%7D%5E%7Bn%7DF_%7Bi%7D=F_%7B1%7D+F_%7B2%7D+%5Ccdots+F_%7Bn%7D)
Theo Dirichlet, có n+1 số thì luôn luôn tồn tại 2 số có cùng số dư khi chia cho n.
-> Trong n+1 số sigma(m), sigma(m+1),…, sigma(m+n) luôn tồn tại 2 số cùng số dư khi chia cho n.
Mà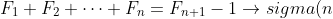=F_%7Bn+2%7D-1)
Giả sử ta “tóm” được 2 số sigma(i) và sigma(j) có cùng số dư khi chia cho n (i < j).
Số này chia hết cho n -> Ta bốc được hẳn 1 đoạn liên tiếp các số Fibonacci F(i+1), F(i+2),…, F(j) mà%5Cvdots&space;n)
Bài toán trở nên dễ ẹc: Tìm j > i (i có sẵn từ đề bài) sao cho
F(j+2) - F(i+1)chia hết cho n, tức là ta sẽ lấy dãy từ F(i) đến F(j).Một điều đáng mừng là
jkhông chạy quái + n(theo trên), limit của n không quá to (n <= 10^6) nên ta tìm chỉ số j bằng cách for trâu.Vì i to (i <= 10^15) nên ta tính số Fibonacci mod n bằng nhân ma trận. Đây là 1 thứ mà học sinh lớp 12 bình thường không hề được học đến, và cũng không bao giờ nghĩ đến luôn. Vì ta cần xét tính chất chia hết với n nên ta tính số Fibonacci theo mod n luôn.
Lưu ý một chút, ta chỉ cần tính F(i) và F(i+1) bằng nhân ma trận, còn lại ta tính các F khác bằng cách lưu vào mảng và tính dựa vào 2 phần tử trước.
Độ phức tạp chỉ còn O(T*(log(n+i)+n)) nếu ta lưu các số Fibonacci vào mảng, thuật toán chạy tốt trong 1s.
P/s: Giờ mới biết codecogs cho chỉnh background của image. Trước giờ toàn để transparent nên nhìn ảnh trên background đen của diễn đàn đến đau cả mắt :’(
P/s2: Quên mất đề multitest sửa chút thuật toán để giảm thời gian cho sống sót qua test mạnh.
P/s3: Cảm ơn anh rogp10 đã chỉ cho em lỗi sai ở công thức Có một chút thay đổi nhỏ ở post, tuy vậy không làm mất đi ý tưởng về thuật toán.
CẢm ơn bác đã chép đề đầy đủ cho em hic
bác @noname00 còn học phổ thông không mà giỏi phết thế
Bài này dễ mà, kiến thức cần thiết toàn basic, đâu nhất thiết còn phải học phổ thông mới làm được
Căn bản tại trí nhớ mình ok nên vẫn còn nhớ.
Hi HK boy
Định nghĩa tập con không nói gì đến việc liên tiếp.
Trong ví dụ tập {F5; F7} là một nghiệm.
P/S Ý tuởng tính trên phần dư khá hay khi thay vi tính tực tiếp giá trị Fn thì ta tính phần dư Fn % n dựa trên phần dư Fn-1%n và Fn-2%n. Và giá trị khởi đầu tính bằng ma trận cung là một cách hay.
https://www.nayuki.io/page/fast-fibonacci-algorithms
Ai cấm mình lấy liên tiếp chứ :v
Nhưng với limit như vậy thì việc lấy liên tiếp có lợi hơn rất nhiều.
Hi HK boy.
Liên tiếp là bài toán con của bài toán ban đầu. Như vậy có thể dẫn đến tìm thiếu nghiệm (bài toán liên tiếp không có nghiệm nhưng bài toán đã cho có nghiệm).
VD
chuỗi 5, 8, 13 tìm tập con có tổng chia hết cho 9.
Không bao giờ vô nghiệm đâu. Mình đã chứng minh là bài toán luôn có nghiệm mà.
Hi HK boy.
Với đầu vào n = 3, i = 5, k = 9. Bài toán đầu có nghiệm {F5, F7}. Không có nghiệm liên tiếp.
Bạn không đọc kĩ đề rồi.
Hi HK boy.
Um mình nhâm. Nhưng như vậy sao pass được ví dụ ?
10 3 9 -> Lấy F(3), F(4), F(5), F(6) (= 2, 3, 5, 8)
Hi HK boy.
Đó là một nghiệm nhưng nó không pass qua nếu out như ví dụ @_@!
Theo đề
Những đề dạng này luôn luôn chỉ cần in ra 1 nghiệm, nghiệm nào cũng được.
Thầy em bảo là dãy fibonacci này chỉ cần vòng lặp đơn giản là while do . ^^ với for to do cùng lắm thì if
Bạn nhìn con số trong đề bài (pdf) nhé mà đề trên là của THPT.
Công thức không đúng phải là F[n+2] - 1.
Có thể dùng quy nạp hoặc telescoping. Ta có F[3] = 2 nên thay vào ra 2 - 1 = 1 okie, vậy P(1) đúng. Giả sử P(k) đúng vậy P(k+1) <=> F[k+2] - 1 + F[k+1] = F[(k+1)+2] - 1 = F[k+3] - 1 luôn đúng.
Dễ thấy với r>=0 thì S(i+r) - S(i-1) = sigma(w in [i…i+r]) F[w]. Vậy ta dùng “hashing” (mod k), đưa chỉ số vào từ i+2 đến i+n+1, cứ đụng hash là out => AC.
Làm while do với for thường thì xác định gãy răng nhé chạy lâu lắm đấy. Có khi đến già vẫn chưa thấy kết quả đâu.
Dạ để em sửa lại ạ.
Phép nhân ma trận với Fibo: [1 1 | 1 0] * [F_1] | F_0] = [F_2 | F_1], hay [F_(n+1) | F_n] = [1 1 | 1 0]^n * [1 | 0]. Từ đây ta thiết lập đẳng thức ma trận Q_n = [1 1 | 1 0] ^ n = [F_(n+1) F_n | F_n F_(n-1)] (n nguyên dương) dễ dàng. (kiểm tra: F_1 = 1, F_0 = 0) vì [1 | 0] là vector cột của Q_1.
Ta có 1 kết quả đẹp mắt: F_(2n) = F_(n+1)^2 - F_(n-1)^2 dùng hđtđn sẽ trở thành F_(2n) = F_(n) * (F_(n+1) + F_(n-1)). Để tính F_(2n) ta sẽ tính Q_(2n) = Q_n^2, vậy F_(2n) = F_(n+1)F_n + F_n*F_(n-1), đpcm
[spoiler](Do F_(2n) nằm ở dòng 1 cột 2 nên ta lấy vector dòng 1 nhân với vector cột 2, rồi nhìn dòng 1 thôi) [/spoiler]
Bạn đọc có thể chứng minh bằng tổ hợp nó cũng có liên quan chút chút đến qhđ với công thức truy hồi đã có sẵn. [spoiler]tức là bây h từ lời giải đặt ra bài toán ứng với nó, chứng minh bằng tổ hợp là như vậy.[/spoiler]
Ma trận thì dễ tính: 8 phép nhân hai số với mỗi phép nhân ma trận (hai cột), mà bài này nhân mod k O(1) nên phần tính F_n mod k là O(logn). Cộng thêm phần hash O(k) nữa là O(k+logn). Tính theo ct truy hồi thì ta có T(2n) = 2T(n) + O(1), hay T(n) = O(n), không nên.